题目内容
11.下列几组数中,是勾股数的有( )①0.6,0.8,1;②5,12,13;③6,8,10;④$\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$.
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
分析 欲判断是否为勾股数,必须根据勾股数是正整数,同时还需验证两小边的平方和是否等于最长边的平方.
解答 解:①0.62+0.82=12,能构成直角三角形,但不是正整数,因此不是勾股数;
②52+122=132,能构成直角三角形,是正整数,因此是勾股数;
③62+82=102,能构成直角三角形,是正整数,因此是勾股数;
④($\frac{1}{3}$)2+($\frac{1}{4}$)2≠($\frac{1}{5}$)2,不能构成直角三角形,不是正整数,因此不是勾股数;
共2组勾股数,
故选:B.
点评 此题主要考查了勾股数的定义,及勾股定理的逆定理:已知△ABC的三边满足a2+b2=c2,则△ABC是直角三角形.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
18.下列方程中配方中有错误的是( )
| A. | x2-4x-1=0化为(x-2)2=5 | B. | x2+6x+8=0化为(x+3)2=1 | ||
| C. | 2x2-7x-6=0化为${(x-\frac{7}{4})^2}=\frac{97}{8}$ | D. | 3x2-4x-2=0化为${(x-\frac{2}{3})^2}=\frac{10}{9}$ |
 ,其
,其
 把二次函数y=$\frac{1}{2}$x2-3x+4配方成y=a(x-k)2+h的形式,并求出它的图象的顶点坐标、对称轴方程,并画出图象.
把二次函数y=$\frac{1}{2}$x2-3x+4配方成y=a(x-k)2+h的形式,并求出它的图象的顶点坐标、对称轴方程,并画出图象.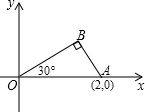 如图,将一块三角板放在平面直角坐标系中,已知∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
如图,将一块三角板放在平面直角坐标系中,已知∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).