题目内容
下框中是小明对一道题目的解答以及老师的批改.

小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?
请指出小明解答中存在的问题,并补充缺少的过程.

小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?
请指出小明解答中存在的问题,并补充缺少的过程.
考点:一元二次方程的应用
专题:几何图形问题
分析:根据题意可得小明没有说明矩形蔬菜种植区域的长与宽之比为2:1的理由,所以应设矩形蔬菜种植区域的宽为xm,则长为2xm,然后由题意得
,矩形蔬菜种植区域的长与宽之比为2:1,再利用小明的解法求解即可.
| 2y-3-1 |
| y-1-1 |
解答:解:小明没有说明矩形蔬菜种植区域的长与宽之比为2:1的理由.
在“设矩形蔬菜种植区域的宽为xm,则长为2xm.”前补充以下过程:
设温室的宽为ym,则长为2ym.
则矩形蔬菜种植区域的宽为(y-1-1)m,长为(2y-3-1)m.
∵
=
=2,
∴矩形蔬菜种植区域的长与宽之比为2:1.
在“设矩形蔬菜种植区域的宽为xm,则长为2xm.”前补充以下过程:
设温室的宽为ym,则长为2ym.
则矩形蔬菜种植区域的宽为(y-1-1)m,长为(2y-3-1)m.
∵
| 2y-3-1 |
| y-1-1 |
| 2y-4 |
| y-2 |
∴矩形蔬菜种植区域的长与宽之比为2:1.
点评:此题考查了一元二次方程的应用.此题属于阅读性题目,注意理解题意,读懂题目是解此题的关键.

练习册系列答案
相关题目
设a>b>0,c为常数,给出下列不等式①a-b>0;②ac>bc;③
<
;④b2>ab,其中正确的不等式有( )
| 1 |
| a |
| 1 |
| b |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,点D、E分别在AB、AC上,且DE∥BC,∠A=30°,∠B=100°,则∠AED的度数是( )
如图,点D、E分别在AB、AC上,且DE∥BC,∠A=30°,∠B=100°,则∠AED的度数是( )| A、30° | B、100° |
| C、130° | D、50° |
在平面直角坐标系中,以点(2,3)为圆心、3为半径的圆,一定( )
| A、与x轴相切,与y轴相切 |
| B、与x轴相切,与y轴相交 |
| C、与x轴相交,与y轴相切 |
| D、与x轴相交,与y轴相交 |
若关于x的方程
-
=1有增根,则m的值是( )
| m |
| x-1 |
| x |
| x-1 |
| A、3 | B、2 | C、1 | D、0 |

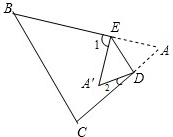 如图,把△ABC纸片沿DE折叠,点A落在四边形BCDE内部.
如图,把△ABC纸片沿DE折叠,点A落在四边形BCDE内部. 如图所示,已知四边形ABCD内接于⊙O,A是弧BAC的中点,AE⊥AC于A,与⊙O及CB的延长线分别交于点F、E,且BF=AD,EM切⊙O于M.
如图所示,已知四边形ABCD内接于⊙O,A是弧BAC的中点,AE⊥AC于A,与⊙O及CB的延长线分别交于点F、E,且BF=AD,EM切⊙O于M.