题目内容
10.已知:$\frac{a}{5}$=$\frac{b}{7}$=$\frac{c}{8}$,且3a-2b+c=27,求2a+4b-3c的值.分析 设$\frac{a}{5}$=$\frac{b}{7}$=$\frac{c}{8}$=k,表示出a,b,c,代入3a-2b+c=27中计算求出k的值,进而求出a,b,c的值,代入原式计算即可得到结果.
解答 解:设$\frac{a}{5}$=$\frac{b}{7}$=$\frac{c}{8}$=k,得到a=5k,b=7k,c=8k,
代入3a-2b+c=27中得:15k-14k+8k=27,
解得:k=3,即a=15,b=21,c=24,
则原式=30+84-72=42.
点评 此题考查了比例的性质,熟练掌握比例的性质是解本题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
1.一长方形的一边长为5a-6b,另一边比它小3a-b,则它的周长是( )
| A. | 14a-22b | B. | 14a+22b | C. | 7a+11b | D. | 7a-11b |
5.若关于x 的一元二次方程(m-2)2x2+(2m+1)x+1=0有解,那么m的取值范围是( )
| A. | m>$\frac{3}{4}$ | B. | m≥$\frac{3}{4}$ | C. | m>$\frac{3}{4}$且m≠2 | D. | m≥$\frac{3}{4}$且m≠2 |
15.下列不是表示数据离散程度的量是( )
| A. | 方差 | B. | 极差 | C. | 平均数 | D. | 标准差 |
2.关于x的方程|x2-2|=m-x有3个互不相同的解,则m的最大值为( )
| A. | $\frac{9}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{9}{4}$ | D. | $\frac{7}{2}$ |
19.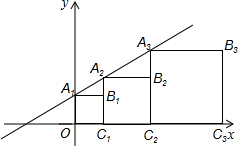 如图,坐标系中的正方形A1OC1B1,A2C1C2B2,A3C2C3B3,…的一边在x轴上,顶点A1,A2,A3,…在直线y=x+1上.
如图,坐标系中的正方形A1OC1B1,A2C1C2B2,A3C2C3B3,…的一边在x轴上,顶点A1,A2,A3,…在直线y=x+1上.
(1)将下列表格补充完整:
(2)写出第4个正方形的边长,并猜想第n个正方形的边长(用含n的代数式表示)
 如图,坐标系中的正方形A1OC1B1,A2C1C2B2,A3C2C3B3,…的一边在x轴上,顶点A1,A2,A3,…在直线y=x+1上.
如图,坐标系中的正方形A1OC1B1,A2C1C2B2,A3C2C3B3,…的一边在x轴上,顶点A1,A2,A3,…在直线y=x+1上.(1)将下列表格补充完整:
| 坐标 | A1(0,1) | A2(1, 2) | A3( 3, 4) |
| 正方形边长 | A1OC1B1:1 | A2C1C2B2: 2 | A3C2C3B3: 4 |
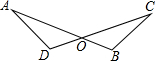 如图,已知AB与CD相交于点O,且AB=CD,当满足OB=OD时,AD=BC.(只需填出一个条件)
如图,已知AB与CD相交于点O,且AB=CD,当满足OB=OD时,AD=BC.(只需填出一个条件)