题目内容
2.关于x的方程|x2-2|=m-x有3个互不相同的解,则m的最大值为( )| A. | $\frac{9}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{9}{4}$ | D. | $\frac{7}{2}$ |
分析 画出函数y=|x2-2|的图象与y=-x+m图象,由图象可知直线y=-x+m经过点($\sqrt{2}$,0)时,方程有3个互不相同的解,可得m=$\sqrt{2}$;当直线y=-x+m在0<x<$\sqrt{2}$时,与y=2-x2只有一个交点时,方程有3个互不相同的解,即可得x2-x+m-2=0有两个相等实数根,由根的判别式可得m的值.
解答 解:如图,方程|x2-2|=m-x的解即函数y=|x2-2|的图象与y=-x+m图象交点的横坐标,
而直线y=-x+m可由y=-x平移|m|个单位得到,
当直线y=-x+m经过点($\sqrt{2}$,0)时,方程有3个互不相同的解,可得m=$\sqrt{2}$;
当直线y=-x+m在0<x<$\sqrt{2}$时,与y=2-x2只有一个交点时,方程有3个互不相同的解,
∴方程2-x2=m-x,即x2-x+m-2=0有两个相等实数根,
∴△=1-4(m-2)=0,
解得:m=$\frac{9}{4}$,
故选:C.
点评 本题主要考查一元二次方程的解,将方程的解转化为函数图象交点问题是解题的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
12.下列说法错误的是( )
| A. | 投掷一枚均匀的骰子,朝上一面的点数是3的概率是$\frac{1}{3}$ | |
| B. | 不可能事件发生的概率为0 | |
| C. | 买一张彩票中奖是随机事件 | |
| D. | 一个事件发生的概率为1%,这件事件就有可能发生 |
13.一个长方形的周长为6a+8b,其中一边长为2a-b,则另一边长为( )
| A. | 4a+5b | B. | a+b | C. | a+5b | D. | a+7b |
17. 如图所示,一棵大树高8米,一场大风过后,大树在离地面3米处折断倒下,树的顶端落在地上,则此时树的顶端离树的底部有( )米.
如图所示,一棵大树高8米,一场大风过后,大树在离地面3米处折断倒下,树的顶端落在地上,则此时树的顶端离树的底部有( )米.
 如图所示,一棵大树高8米,一场大风过后,大树在离地面3米处折断倒下,树的顶端落在地上,则此时树的顶端离树的底部有( )米.
如图所示,一棵大树高8米,一场大风过后,大树在离地面3米处折断倒下,树的顶端落在地上,则此时树的顶端离树的底部有( )米.| A. | 4 | B. | 3.5 | C. | 5 | D. | 13.6 |
11.如图,已知△ABC的六个元素,则如图甲、乙、丙三个三角形中和△ABC全等的图形是( )


| A. | 甲和丙 | B. | 乙和丙 | C. | 只有乙 | D. | 只有丙 |
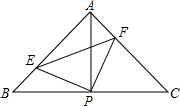 如图,已知△ABC中,AB=AC=2,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论:
如图,已知△ABC中,AB=AC=2,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE、PF分别交AB、AC于点E、F,给出以下四个结论: 如图,矩形ABCO中,点B的坐标为(4,2),点E为AB边上的一点,坐标为(1,2),点M为y轴负半轴上一动点,点N为x轴正半轴上一动点,且∠MEN=90°,在直线y=-10x+60上找点F,使∠BEF=∠EMN,请直接写出点F的坐标.
如图,矩形ABCO中,点B的坐标为(4,2),点E为AB边上的一点,坐标为(1,2),点M为y轴负半轴上一动点,点N为x轴正半轴上一动点,且∠MEN=90°,在直线y=-10x+60上找点F,使∠BEF=∠EMN,请直接写出点F的坐标.