题目内容
20.方程7x2-(k+13)x+k2-k-2=0(k是常数)有两实根α、β,且0<α<1,1<β<2,求k的取值范围.分析 令y=7x2-(k+13)x+k2-k-2,根据方程的两实数根α、β的范围,即可得出关于k的一元二次不等式组,解不等式组即可得出结论.
解答 解:令y=7x2-(k+13)x+k2-k-2,
∵方程7x2-(k+13)x+k2-k-2=0(k是常数)有两实根α、β,
∴抛物线y=7x2-(k+13)x+k2-k-2与x轴有两个交点,
∵0<α<1,1<β<2,a=7>0,
∴$\left\{\begin{array}{l}{{k}^{2}-k-2>0}\\{7-(k+13)+{k}^{2}-k-2<0}\\{28-2(k+13)+{k}^{2}-k-2>0}\end{array}\right.$,
解得:-2<k<-1或3<4.
点评 本题考查了抛物线与x轴的交点,将方程的解转化为抛物线与x轴的交点的横坐标是解题的关键.

练习册系列答案
相关题目
11.如图,已知△ABC的六个元素,则如图甲、乙、丙三个三角形中和△ABC全等的图形是( )


| A. | 甲和丙 | B. | 乙和丙 | C. | 只有乙 | D. | 只有丙 |
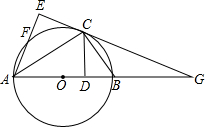 如图,在Rt△AEG中,∠E=90°,∠EAG的平分数交EG于C,过C作AC的垂线交AG于B,以AB为直径的⊙O交AE于F
如图,在Rt△AEG中,∠E=90°,∠EAG的平分数交EG于C,过C作AC的垂线交AG于B,以AB为直径的⊙O交AE于F 把下列各数在数轴上表示出来,并用“<”把它们连接起来.
把下列各数在数轴上表示出来,并用“<”把它们连接起来. 如图,矩形ABCO中,点B的坐标为(4,2),点E为AB边上的一点,坐标为(1,2),点M为y轴负半轴上一动点,点N为x轴正半轴上一动点,且∠MEN=90°,在直线y=-10x+60上找点F,使∠BEF=∠EMN,请直接写出点F的坐标.
如图,矩形ABCO中,点B的坐标为(4,2),点E为AB边上的一点,坐标为(1,2),点M为y轴负半轴上一动点,点N为x轴正半轴上一动点,且∠MEN=90°,在直线y=-10x+60上找点F,使∠BEF=∠EMN,请直接写出点F的坐标.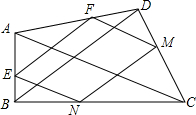 如图,在四边形ABCD中,∠ABC=90°,点E,F,M,N分别在AB,AD,DC,CB边上,连接EF,EN,NM,FM,若EF∥BD∥NM,$\frac{EN}{AC}$+$\frac{EF}{BD}$=1.
如图,在四边形ABCD中,∠ABC=90°,点E,F,M,N分别在AB,AD,DC,CB边上,连接EF,EN,NM,FM,若EF∥BD∥NM,$\frac{EN}{AC}$+$\frac{EF}{BD}$=1.