题目内容
13.如图在一个边长为a的小正方形中,剪去一个边长为b的小正方形,再将余下的部分拼成一个长方形.(1)两个图形(着色部分)的面积之间有什么关系?
(2)请结合图形,对平方差公式(a+b)(a-b)=a2-b2进行解释.

| 算式 | 与平方差公式a对应的项 | 与平方差公式中b对应的项 | 写成a2-b2的形式 | 计算结果 |
| (x+y)(x-y) | x | y | x2-y2 | x2-y2 |
| (m+3)(m-3) | m | 3 | m2-32 | m2-9 |
| (2x+1)(2x-1) | 2x | 1 | (2m)2-12 | 4m2-1 |
| (x+2y)(-x+2y) | x | 2y | x2-(2y)2 | x2-4y2 |
分析 (1)两个图形只是位置改变,因而面积相等;
(2)利用两种方法表示阴影部分是面积,据此即可证明公式.
解答 解:(1)两个图形(着色部分)的面积相等;
(2)第一个图形中阴影部分的面积是a2-b2,第二个图形的面积是(a+b)(a-b).
则(a+b)(a-b)=a2-b2.
| 算式 | 与平方差公式a对应的项 | 与平方差公式中b对应的项 | 写成a2-b2的形式 | 计算结果 |
| (x+y)(x-y) | x | y | x2-y2 | x2-y2 |
| (m+3)(m-3) | m | 3 | m2-32 | m2-9 |
| (2x+1)(2x-1) | 2x | 1 | (2m)2-12 | 4m2-1 |
| (x+2y)(-x+2y) | x | 2y | x2-(2y)2 | x2-4y2 |
点评 此题主要考查的是平方差公式的几何表示,运用不同方法表示阴影部分面积是解题的关键.

练习册系列答案
相关题目
3.若x<0,则|$\sqrt{{x}^{2}}$+3x|=( )
| A. | -4x | B. | 4x | C. | -2x | D. | 2x |
2. 如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
 如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
如图,已知直线a、b被直线c所截,那么∠1的同位角是( )| A. | ∠2 | B. | ∠3 | C. | ∠4 | D. | ∠5 |
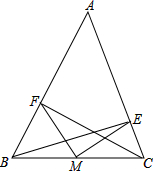 如图所示,BE,CF是△ABC的两条高,M为BC中点,连接MF,ME.
如图所示,BE,CF是△ABC的两条高,M为BC中点,连接MF,ME.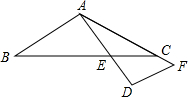 如图,在△ABC中,AB=AC,将AB边绕点A按逆时针方向旋转90°,得到线段AD,AD交BC边于点E,过点D作AD的垂线,交AC边的延长线于点F,若AE=9,DF=8,则线段DE的长为6.
如图,在△ABC中,AB=AC,将AB边绕点A按逆时针方向旋转90°,得到线段AD,AD交BC边于点E,过点D作AD的垂线,交AC边的延长线于点F,若AE=9,DF=8,则线段DE的长为6.