题目内容
1.己知抛物线y1=-x2+1,直线y2=x+1,当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M,若y1=y2,记M=y1=y2,例如:当x=1时,y1=0,y2=2,y1<y2,此时M=0,下列判断:①当x<0时,x值越大,M值越小;
②使得M大于1的x值不存在;
③使得M=$\frac{1}{2}$的x值是-$\frac{{\sqrt{2}}}{2}$或$\frac{{\sqrt{2}}}{2}$;
④使得M=$\frac{1}{2}$的x值是-$\frac{1}{2}$或$\frac{{\sqrt{2}}}{2}$,
其中正确的是( )
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
分析 ①错误.观察图象可知当x<0时,x值越大,M值越大.
②正确.因为y1=-x2+1的最大值为1,所以使得M大于1的x值不存在.
③错误.使得M=$\frac{1}{2}$的x值是-$\frac{1}{2}$或$\frac{{\sqrt{2}}}{2}$.
④正确.求出x=-$\frac{1}{2}$和$\frac{\sqrt{2}}{2}$时y的值即可判断.
解答 解:①错误.观察图象可知当x<0时,x值越大,M值越大.故①错误.
②正确.因为y1=-x2+1的最大值为1,所以使得M大于1的x值不存在,故②正确.
③错误.使得M=$\frac{1}{2}$的x值是-$\frac{1}{2}$或$\frac{{\sqrt{2}}}{2}$,故错误.
④正确.∵x=-$\frac{1}{2}$时,y1=$\frac{3}{4}$,y2=$\frac{1}{2}$,∴M=$\frac{1}{2}$,
∵x=$\frac{\sqrt{2}}{2}$时,y1=$\frac{1}{2}$,y2=$\frac{\sqrt{2}}{2}$+1,∴M=$\frac{1}{2}$.
故选D.
点评 本题考查二次函数与不等式等知识,解题的关键是理解题意,学会画出函数图象,利用图象解决问题,所以中考常考题型.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
12. 用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)
用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)
(1)求S关于x的函数解析式及x的取值范围
(2)写出下面表格中与x相对应的S的值
(3)猜一猜,当x为何值时,S的值最大?
 用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)
用40cm长的绳子围成矩形ABCD,设AB=xm,矩形ABCD的面积为S(m2)(1)求S关于x的函数解析式及x的取值范围
(2)写出下面表格中与x相对应的S的值
| x | … | 8 | 9 | 9.5 | 10 | 10.5 | 11 | 12 | … |
| S | … | 96 | 99 | 99.75 | 100 | 99,75 | 99 | 96 | … |
13.如图在一个边长为a的小正方形中,剪去一个边长为b的小正方形,再将余下的部分拼成一个长方形.
(1)两个图形(着色部分)的面积之间有什么关系?
(2)请结合图形,对平方差公式(a+b)(a-b)=a2-b2进行解释.

(1)两个图形(着色部分)的面积之间有什么关系?
(2)请结合图形,对平方差公式(a+b)(a-b)=a2-b2进行解释.

| 算式 | 与平方差公式a对应的项 | 与平方差公式中b对应的项 | 写成a2-b2的形式 | 计算结果 |
| (x+y)(x-y) | x | y | x2-y2 | x2-y2 |
| (m+3)(m-3) | m | 3 | m2-32 | m2-9 |
| (2x+1)(2x-1) | 2x | 1 | (2m)2-12 | 4m2-1 |
| (x+2y)(-x+2y) | x | 2y | x2-(2y)2 | x2-4y2 |
 如图,求图中x的值.
如图,求图中x的值.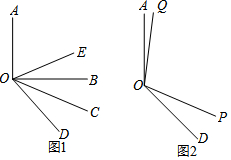
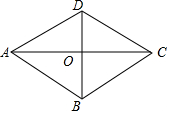 已知?ABCD的对角线AC,BD相交于点O,AD=$\sqrt{13}$,AC=6,BD=4,你认为四边形ABCD是菱形吗?请说明理由.
已知?ABCD的对角线AC,BD相交于点O,AD=$\sqrt{13}$,AC=6,BD=4,你认为四边形ABCD是菱形吗?请说明理由.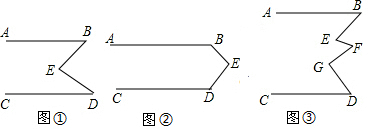
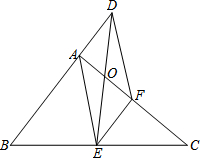 在Rt△ABC中,∠BAC=90°,E、F分别是BC、AC的中点,延长BA到点D,使AB=2AD,连接DE、DF、AE、EF,AF与DE交于点O.
在Rt△ABC中,∠BAC=90°,E、F分别是BC、AC的中点,延长BA到点D,使AB=2AD,连接DE、DF、AE、EF,AF与DE交于点O.