题目内容
8.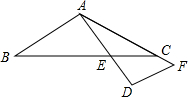 如图,在△ABC中,AB=AC,将AB边绕点A按逆时针方向旋转90°,得到线段AD,AD交BC边于点E,过点D作AD的垂线,交AC边的延长线于点F,若AE=9,DF=8,则线段DE的长为6.
如图,在△ABC中,AB=AC,将AB边绕点A按逆时针方向旋转90°,得到线段AD,AD交BC边于点E,过点D作AD的垂线,交AC边的延长线于点F,若AE=9,DF=8,则线段DE的长为6.
分析 过EG∥AB交AF于G,如图,设DE=x,由旋转的性质得∠BAD=90°,AB=AD=9+x,则AC=9+x,再证明△AEG∽△ADF,利用相似比可表示出EG=$\frac{72}{9+x}$,接着证明GC=GE=$\frac{72}{9+x}$,于是AG=9+x-$\frac{72}{9+x}$,然后在Rt△AEC中利用勾股定理得到92+($\frac{72}{9+x}$)2=(9+x-$\frac{72}{9+x}$)2,整理得(9+x)2=225,再解方程即可得到DE的长.
解答 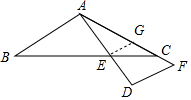 解:过EG∥AB交AF于G,如图,设DE=x,
解:过EG∥AB交AF于G,如图,设DE=x,
∵把AB边绕点A按逆时针方向旋转90°,得到线段AD,
∴∠BAD=90°,AB=AD=9+x,
∴AC=9+x,
∵AD⊥DF,
∴∠ADF=90°,
∴AB∥DF,
∴EG∥DF,
∴△AEG∽△ADF,
∴$\frac{EG}{DF}$=$\frac{AE}{AD}$,即$\frac{EG}{8}$=$\frac{9}{9+x}$,解得EG=$\frac{72}{9+x}$,
∵EG∥AB,
∴∠GEC=∠B,
而AB=AC,
∴∠B=∠ACB,
∴∠GEC=∠GCE,
∴GC=GE=$\frac{72}{9+x}$,
∴AG=AC-GC=9+x-$\frac{72}{9+x}$,
在Rt△AEC中,92+($\frac{72}{9+x}$)2=(9+x-$\frac{72}{9+x}$)2,
整理得(9+x)2=225,解得x1=6,x2=-24(舍去),
即DE的长为6.
故答案为6.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰三角形的性质和相似三角形的判定与性质.

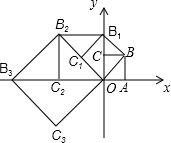 如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2015的坐标为( )
如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OB1为边作第三个正方形OB1B2C2,照此规律作下去,则点B2015的坐标为( )| A. | (21008,0) | B. | (21007,-21007) | C. | (21009,21009) | D. | (-21007,21007) |
(1)两个图形(着色部分)的面积之间有什么关系?
(2)请结合图形,对平方差公式(a+b)(a-b)=a2-b2进行解释.

| 算式 | 与平方差公式a对应的项 | 与平方差公式中b对应的项 | 写成a2-b2的形式 | 计算结果 |
| (x+y)(x-y) | x | y | x2-y2 | x2-y2 |
| (m+3)(m-3) | m | 3 | m2-32 | m2-9 |
| (2x+1)(2x-1) | 2x | 1 | (2m)2-12 | 4m2-1 |
| (x+2y)(-x+2y) | x | 2y | x2-(2y)2 | x2-4y2 |
 已知函数y=kx+b(k≠0)的图象如图,则y=-2kx+b(k≠0)的图象可能是( )
已知函数y=kx+b(k≠0)的图象如图,则y=-2kx+b(k≠0)的图象可能是( )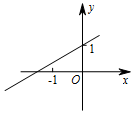
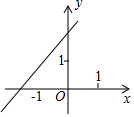
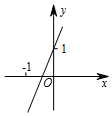
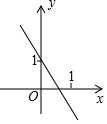
 如图,在直角坐标系中,点A是反比例函数y1=$\frac{k}{x}$图象上一点,AB⊥x轴的正半轴于点B,点C是OB的中点,一次函数y2=ax+b的图象经过A、C两点,交y轴于点D(0,-2),△AOB的面积为4
如图,在直角坐标系中,点A是反比例函数y1=$\frac{k}{x}$图象上一点,AB⊥x轴的正半轴于点B,点C是OB的中点,一次函数y2=ax+b的图象经过A、C两点,交y轴于点D(0,-2),△AOB的面积为4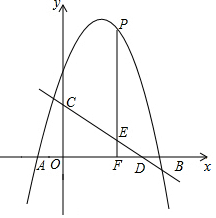 如图,抛物线y=-x2+4x+5与x轴交于A,B两点(点A在点B的左侧),直线y=$-\frac{3}{4}x+3$与y轴交于点C,与x轴交于点D.P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.
如图,抛物线y=-x2+4x+5与x轴交于A,B两点(点A在点B的左侧),直线y=$-\frac{3}{4}x+3$与y轴交于点C,与x轴交于点D.P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E,设点P的横坐标为m.