题目内容
16.下列说法:①若关于x的方程x2-(a-3)x-3a-b2=0有两个相等的实数根,则关于的方程x2+ax+b=0的两根分别是x1=0,x2=3;
②若b=2a+c,则一元二次方程ax2+bx+c=0有两个不相等的实数根;
③若m、n(m<n)是关于x的方程1-(x-a)(x-b)=0的两根,且a<b,则a,b,m,n的大小关系是m<a<b<n,
其中正确的有( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
分析 ①根据根的判别式求得a=-3,b=0,把a=-3,b=0代入x2+ax+b=0得:x2-3x=0,解得x1=0,x2=3;故①正确;
②根据根的判别式求得4a2+c2>0,于是得到一元二次方程ax2+bx+c=0有两个不相等的实数根;故②正确;
③方程变形为(x-a)(x-b)=1,利用二次函数与异次函数图象解决问题:二次函数y=(x-a)(x-b)与x轴两个交点坐标为(a,0),(b,0),且直线y=1与抛物线y=(x-a)(x-b)的交点的横坐标分别为m与n,于是可得到则a、b、m、n的大小关系.
解答 解:①∵关于x的方程x2-(a-3)x-3a-b2=0有两个相等的实数根,
∴△=[-(a-3)]2-4(-3a-b2)=(a+3)2+4b2=0,
∴a=-3,b=0,
把a=-3,b=0代入x2+ax+b=0得:x2-3x=0,
解得:x1=0,x2=3;故①正确;
②∵△=b2-4ac,b=2a+c,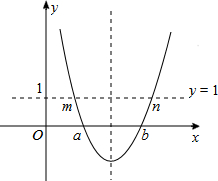
∴△=(2a+c)2-4ac=4a2+c2,
∵a≠0,
∴4a2+c2>0,
∴一元二次方程ax2+bx+c=0有两个不相等的实数根;故②正确;
③如图,∵1-(x-a)(x-b)=0,
∴(x-a)(x-b)=1,
∵二次函数y=(x-a)(x-b)与x轴两个交点坐标为(a,0),(b,0),
则直线y=1与抛物线y=(x-a)(x-b)的交点的横坐标分别为m与n,
∴m<a<b<n,故③正确.
故选D.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了图象法解决数学问题.

练习册系列答案
相关题目