题目内容
8．半径为2cm的圆内接正方形的对角线长为4cm，面积为8cm2．分析 由正方形的性质得出BD、AC是直径，求出对角线的长，即可得出正方形的面积．
解答 解：如图所示：
∵四边形ABCD是⊙O的内接正方形，
∴∠BAD=∠ABC=90°，BD=AC，
∴BD、AC是直径，
∴BD=AC=2×2=4（cm），
∴正方形ABCD的面积=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×4×4=8（cm2），
故答案为4，8．
点评 该题主要考查了圆内接正方形的性质及其应用问题；由正方形的性质得出对角线为直径是解决问题的关键．
练习册系列答案
相关题目
18．先列方程，在估算出方程的解
甲型钢笔每支3元，乙型钢笔每支5元，用40元钱买了两种钢笔共10支，还多2元，问两种钢笔各买了多少支？
解：设买了甲型铅笔x支，则乙型钢笔10-x支，依题意得方程：3x+5（10-x）=40-2．
这里x＞0，列表如下：
从表中看出x=6是原方程的解．
甲型钢笔每支3元，乙型钢笔每支5元，用40元钱买了两种钢笔共10支，还多2元，问两种钢笔各买了多少支？
解：设买了甲型铅笔x支，则乙型钢笔10-x支，依题意得方程：3x+5（10-x）=40-2．
这里x＞0，列表如下：
| x（支） | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3x+5（10-x）（元） | 48 | 46 | 44 | 42 | 40 | 38 | 36 | 34 |
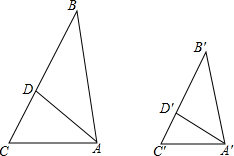如图，AD，A′D′分别为△ABC和△A′B′C′的角平分线，且AB：A′B′=BD：B′D′=AD：A′D′．试说明：△ABC∽△A′B′C′．