题目内容
7.观察下列等式:$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}-\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}-\frac{1}{4}$
三个等式两边分别相加得:
$\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}$=1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}$=1-$\frac{1}{4}$=$\frac{3}{4}$
(1)猜想并写出:$\frac{1}{n•(n+1)}$$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)直接写出下列各式的计算结果:
$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{1007×1008}$=$\frac{1007}{1008}$;
(3)探究并计算:
$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{2014×2016}$.
分析 (1)观察已知等式,得到拆项规律,写出即可;
(2)利用得出的规律将原式变形,计算即可得到结果;
(3)原式利用程序法变形,计算即可得到结果.
解答 解:(1)根据题意得:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{1007}$-$\frac{1}{1008}$=1-$\frac{1}{1008}$=$\frac{1007}{1008}$;
(3)原式=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{6}$+…+$\frac{1}{2014}$-$\frac{1}{2016}$)=$\frac{1}{2}$($\frac{1}{2}$-$\frac{1}{2016}$)=$\frac{1007}{4032}$.
故答案为:(1)$\frac{1}{n}$-$\frac{1}{n+1}$;(2)$\frac{1007}{1008}$
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
18.先列方程,在估算出方程的解
甲型钢笔每支3元,乙型钢笔每支5元,用40元钱买了两种钢笔共10支,还多2元,问两种钢笔各买了多少支?
解:设买了甲型铅笔x支,则乙型钢笔10-x支,依题意得方程:3x+5(10-x)=40-2.
这里x>0,列表如下:
从表中看出x=6是原方程的解.
甲型钢笔每支3元,乙型钢笔每支5元,用40元钱买了两种钢笔共10支,还多2元,问两种钢笔各买了多少支?
解:设买了甲型铅笔x支,则乙型钢笔10-x支,依题意得方程:3x+5(10-x)=40-2.
这里x>0,列表如下:
| x(支) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3x+5(10-x)(元) | 48 | 46 | 44 | 42 | 40 | 38 | 36 | 34 |
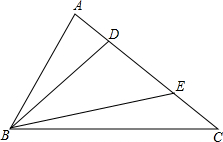 已知△ABC中.∠ABC=60°,D、E为边AC上的两点.DE=4,BD=6,BE=8.∠ABD=20°,∠CBE=10°,试在边AB、BC上分别找一点F、G.使四边形DFGE的周长最短.
已知△ABC中.∠ABC=60°,D、E为边AC上的两点.DE=4,BD=6,BE=8.∠ABD=20°,∠CBE=10°,试在边AB、BC上分别找一点F、G.使四边形DFGE的周长最短.