题目内容
11．
如图，平行四边形中，AE⊥BC于E，AF⊥CD于F．（1）若∠EAF=65°，求∠BAD的度数；
（2）若AE=3cm，BC=5cm，CD=4cm，求AF的长．
分析 （1）由垂线的定义和四边形内角和求出∠C=115°，再由平行四边形的性质得出
（2）根据平行四边形的面积为定值计算即可∴∠BAD=∠C=115°即可．
解答 解：（1）∵AE⊥BC于E，AF⊥CD于F，
∴∠AEC=∠AFC=90°，
∵∠AEC+∠C+∠EAF+∠AFC=360°，∠EAF=65°，
∴∠C=115°，
∵四边形ABCD是平行四边形，
∴∠BAD=∠C=115°；
（2）∵平行四边形的面积=CD•AF=BC•AE，
∴AF=$\frac{BC•AE}{CD}$=$\frac{5×3}{4}$=$\frac{15}{4}$（cm）．
点评 本题考查了平行四边形的性质和平行四边形的面积公式、四边形内角和；熟练掌握平行四边形的性质，熟记平行四边形的面积的计算方法是解决问题（2）的关键．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
1．x=$\sqrt{3}$+1，y=$\sqrt{3}$-1，则（1+$\frac{1}{y}$）（1-$\frac{1}{x}$）=（ ）
| A． | $4\sqrt{3}$ | B． | $\sqrt{3}$ | C． | $2\sqrt{3}$ | D． | $\frac{3}{2}$ |
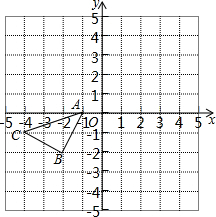如图所示的正方形网格中，△ABC的顶点均在格点上，请在所给直角坐标系中按要求画图和解答下列问题：
如图，在⊙O中，∠C=30°，AB=2cm，则弧AB的长等于$\frac{2π}{3}$．（结果保留π）
如图，在平行四边形ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF：FC=1：2．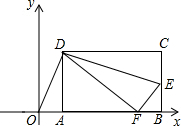
如图，矩形ABCD的顶点AB在x轴上，点D的坐标为（3，4），点E在边BC上，△CDE沿DE翻折后点C恰好落在x轴上点F处，若△ODF为等腰三角形，点C的坐标为（8，4）或（3$+2\sqrt{5}$，4）或（$\frac{43}{6}$，4）．
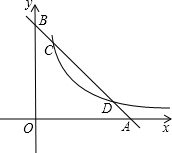已知：一次函数y=-x+b的图象与x轴、y轴的交点分别为A、B与反比例函数$y=\frac{5}{x}（x＞0）$的图象交于点C、D，且$\frac{BD}{BA}=\frac{2}{3}$．
如图，AB是⊙O的直径，弦AD平分∠BAC，交⊙O于点D，DE⊥AC于点E，求证：DE是⊙O的切线．