��Ŀ����
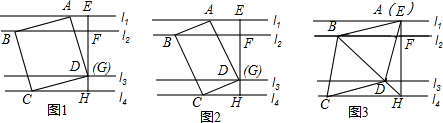
15����֪��l1��l2��l3��l4����E��l1�ϵ�һ�㣬����E��EH��l1���ֱ���l2��l3��l4���ڵ�F��G��H��EF=GH=1��FG=3�����ı���ABCD����ƽ�����У�ʹ���ĸ�����ֱ�����ֱ��l1��l2��l3��l4�ϣ���1����ͼ1�����ı���ABCD�������Σ��ҵ�D���G�غϣ���������ABCD�����Ϊ17��
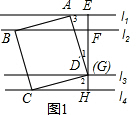
��2����ͼ2�����ı���ABCD�Ǿ��Σ��ҵ�D���G�غϣ�AD=2CD�������ABCD�������
��3����ͼ3�����ı���ABCD�����Σ��ҵ�A���E�غϣ�BD���ӳ��߸պþ�����H��������ABCD�������
���� ��1��������֪�ó���AED�ա�DHC��AAS�������ɵó������εı߳���
��2��������֪�����õ�EH��l4�����ݾ��ε����ʵõ���ADC=90�㣮������ǵ����ʵõ���CDH=��EAD���Ƴ���ADE�ס�DCH���������������ε����ʵõ�$\frac{AE}{HD}=\frac{AD}{CD}$�����AE=2HD=2�����ݹ��ɶ����õ�AD=2$\sqrt{5}$���õ�CD=$\sqrt{5}$�����ɵõ����ۣ�
��3���������ε����ʵõ�AD=CD��AC��BD��BD=2OD����ADB=��CDB������ȫ�������ε����ʵõ�CH=AH=5����DHA=��DHC=45�㣮���ݹ��ɶ����õ�AC=5$\sqrt{2}$����ֱ�������εõ�DH=$\sqrt{2}$��OH=$\frac{5}{2}$$\sqrt{2}$���������ε������ʽ���ɵõ����ۣ�
���  �⣺��1����ͼ1��������ɵã���1+��3=90�㣬��1+��2=90�㣬
�⣺��1����ͼ1��������ɵã���1+��3=90�㣬��1+��2=90�㣬
���2=��3��
�ڡ�AED�͡�DHC�У�$\left\{\begin{array}{l}{��AEF=��DHC=90��}\\{��3=��2}\\{AD=CD}\end{array}\right.$��
���AED�ա�DHC��AAS����
��AE=HD=1��
�֡�DE=1+3=4��
��������ABCD�ı߳�=$\sqrt{{1}^{2}+{4}^{2}}$=$\sqrt{17}$��
��������ABCD�����=17��
�ʴ�Ϊ��17��
��2����l1��l4��EH��l1��
��EH��l4��
���AEG=��GHC=90�㣬
���ı���ABCD�Ǿ��Σ�
���ADC=90�㣮
���ADE+��CDH=90�㣬
�ߡ�ADE+��EAD=90��
���CDH=��EAD��
�֡ߡ�AEG=��GHC��
���ADE�ס�DCH��
��$\frac{AE}{HD}=\frac{AD}{CD}$��
��AD=2CD��
��AE=2HD=2��
�ڡ�ADE�У���AED=90�㣬AE=2��ED=4��
��AD=2$\sqrt{5}$��
��CD=$\sqrt{5}$��
�����ABCD�����Ϊ2$\sqrt{5}$��$\sqrt{5}$=10��
��3����ͼ3������AC��BD�ڵ�O��
���ı���ABCD�����Σ�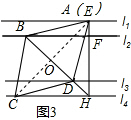
��AD=CD��AC��BD��BD=2OD����ADB=��CDB��
���ADH=��CDH��
�ڡ�ADH���CDH��$\left\{\begin{array}{l}{AD=CD}\\{��ADH=��CDH}\\{DH=DH}\end{array}\right.$��
���ADH�ա�CDH��
��CH=AH=5����DHA=��DHC=45�㣬
��Rt��ACH�У���AHC=90�㣬
��AC=5$\sqrt{2}$��
��l1��l3��EH��l1��
��EH��l3��
���DGH=90�㣬
��Rt��DGH�У�GH=1����DHG=45�㣬
��DH=$\sqrt{2}$��
��Rt��COH�У���COH=90�㣬��OHC=45�㣬CH=5��
��OH=$\frac{5}{2}$$\sqrt{2}$��
��OD=$\frac{3}{2}$$\sqrt{2}$��
��BD=3$\sqrt{2}$��
������ABCD�����=$\frac{1}{2}$��5$\sqrt{2}$��3$\sqrt{2}$=15��
���� ������Ҫ������ƽ���ߵ����ʣ����ɶ�����ȫ�������ε��ж����ԣ����������ε��ж������ʣ����ε�����ļ��㣬����Ӧ��ȫ�������ε��ж������ǽ���ؼ���

 ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
ȫ�ŵ�����Ԫ�ƻ�ϵ�д�| A�� | $\left\{\begin{array}{l}{x+y=1}\\{x-z=2}\end{array}\right.$ | B�� | $\left\{\begin{array}{l}{{y}^{2}-1=0}\\{x-2y=0}\end{array}\right.$ | C�� | $\left\{\begin{array}{l}{y-2x=1}\\{y=5}\end{array}\right.$ | D�� | $\left\{\begin{array}{l}{\frac{1}{x}+3y=0}\\{x-y=1}\end{array}\right.$ |
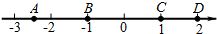 ��ͼ����������A��B��C��D�ĵ㣬���б�ʾ��Ϊ�෴��������ʵ������Ӧ�ĵ��ǣ�������
��ͼ����������A��B��C��D�ĵ㣬���б�ʾ��Ϊ�෴��������ʵ������Ӧ�ĵ��ǣ�������| A�� | ��A���D | B�� | ��A���C | C�� | ��B���D | D�� | ��B���C |
| A�� | 24x2y=3x•8xy | B�� | m2-2m-3=m��m-2��-3 | C�� | x2+2x+1=��x+1��2 | D�� | ��x+3����x-3��=x2-9 |
 ��֪����ͼ��Rt��ABC�У���BAC=90�㣬AB=5��AC=12������ABC������BC����ƽ��m����λ���ȵ���DEF������A��B��C�ֱ���D��E��F��Ӧ�����Ե�A��D��EΪ������������ǵ��������Σ���m��ֵ��$\frac{50}{13}$��5��$\frac{13}{2}$��
��֪����ͼ��Rt��ABC�У���BAC=90�㣬AB=5��AC=12������ABC������BC����ƽ��m����λ���ȵ���DEF������A��B��C�ֱ���D��E��F��Ӧ�����Ե�A��D��EΪ������������ǵ��������Σ���m��ֵ��$\frac{50}{13}$��5��$\frac{13}{2}$��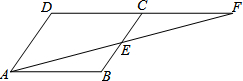 ��ͼ��?ABCD�У�E��BC���е㣬����AE���ӳ���DC���ӳ�����F�����ʣ�AB��CF�������˵�����ɣ�
��ͼ��?ABCD�У�E��BC���е㣬����AE���ӳ���DC���ӳ�����F�����ʣ�AB��CF�������˵�����ɣ�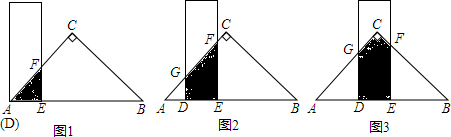
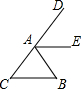 ��ͼ����֪AB=AC��AEƽ�֡�DAB����֤��AE��BC��
��ͼ����֪AB=AC��AEƽ�֡�DAB����֤��AE��BC��