题目内容
16.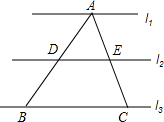 如图,l1∥l2∥l3,其中l1与l2、l2与l3间的距离相等,则下列结论:①BC=2DE;②△ADE∽△ABC;③$\frac{AD}{AE}=\frac{AB}{AC}$.其中正确的有( )
如图,l1∥l2∥l3,其中l1与l2、l2与l3间的距离相等,则下列结论:①BC=2DE;②△ADE∽△ABC;③$\frac{AD}{AE}=\frac{AB}{AC}$.其中正确的有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
分析 根据l1∥l2∥l3判断△ADE∽△ABC,根据相似三角形的性质对所给命题进行判断.
解答 解:l1与l2、l2与l3间的距离为l,则△ADE和△ABC分别是l,2l,
∵l1∥l2∥l3,
∴△ADE∽△ABC,
∴故选项②正确.
∵△ADE∽△ABC,
∴$\frac{AD}{AE}=\frac{AB}{AC}$,
∴故选项③正确,
∵△ADE∽△ABC,
$\frac{DE}{BC}=\frac{l}{2l}=\frac{1}{2}$,
即BC=2DE,
故正确的有3个,
故选:A.
点评 本题考查的是相似三角形的判定与性质,根据根据l1∥l2∥l3判断△ADE∽△ABC,然后用相似三角形的性质判定结论,解题的关键是能判断△ADE∽△ABC.

练习册系列答案
相关题目
4.在3,2,-1,-4这四个数中,比-2小的数是( )
| A. | -4 | B. | -1 | C. | 2 | D. | 3 |
6. 如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )
如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )
 如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )
如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则∠1的度数为( )| A. | 65° | B. | 55° | C. | 45° | D. | 35° |
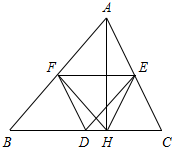 已知:如图,在△ABC中,AH⊥BC于点H,点D,E,F分别是BC,AC,AB的中点.若∠A的度数是α,则图中度数等于α的角还有4个.
已知:如图,在△ABC中,AH⊥BC于点H,点D,E,F分别是BC,AC,AB的中点.若∠A的度数是α,则图中度数等于α的角还有4个.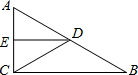 如图,在△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,如果AC=6,AB=10,则△AED的周长=12.
如图,在△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,如果AC=6,AB=10,则△AED的周长=12.