题目内容
7.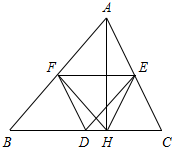 已知:如图,在△ABC中,AH⊥BC于点H,点D,E,F分别是BC,AC,AB的中点.若∠A的度数是α,则图中度数等于α的角还有4个.
已知:如图,在△ABC中,AH⊥BC于点H,点D,E,F分别是BC,AC,AB的中点.若∠A的度数是α,则图中度数等于α的角还有4个.
分析 根据三角形的中位线平行于第三边并且可得DF∥AC,DE∥AB,然后根据平行线的性质求出∠BFD=α,∠FDE=∠BAC=α,∠DEC=∠BAC=α,根据直角三角形斜边上的中线等于斜边的一半可得AF=FH,AE=EH,再根据等边对等角可得∠AHF=∠FAH,∠AHE=∠EAH,从而求出∠FHE=∠BAC=α.
解答 解:∵D,E,F分别为BC,AC,AB的中点,
∴DF∥AC,DE∥AB,
∴∠BFD=∠BAC=α,∠FDE=∠BFD=α,
同理可得∠CED=∠CAB=α,
∵AH⊥BC,E、F分别为AC、AB的中点,
∴AF=FH,AE=EH,
∴∠AHF=∠FAH,∠AHE=∠EAH,
∴∠AHF+∠AHE=∠FAH+∠EAH,
即∠FHE=∠BAC=α,
故答案为4.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半的性质,直角三角形斜边上的中线等于斜边的一半的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.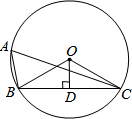 如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )
如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )
 如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )
如图,⊙O的半径为2,点A为⊙O上一点,半径OD⊥弦BC于D,如果∠BAC=60°,那么OD的长是( )| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
16.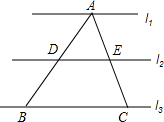 如图,l1∥l2∥l3,其中l1与l2、l2与l3间的距离相等,则下列结论:①BC=2DE;②△ADE∽△ABC;③$\frac{AD}{AE}=\frac{AB}{AC}$.其中正确的有( )
如图,l1∥l2∥l3,其中l1与l2、l2与l3间的距离相等,则下列结论:①BC=2DE;②△ADE∽△ABC;③$\frac{AD}{AE}=\frac{AB}{AC}$.其中正确的有( )
 如图,l1∥l2∥l3,其中l1与l2、l2与l3间的距离相等,则下列结论:①BC=2DE;②△ADE∽△ABC;③$\frac{AD}{AE}=\frac{AB}{AC}$.其中正确的有( )
如图,l1∥l2∥l3,其中l1与l2、l2与l3间的距离相等,则下列结论:①BC=2DE;②△ADE∽△ABC;③$\frac{AD}{AE}=\frac{AB}{AC}$.其中正确的有( )| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
17.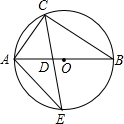 如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
 如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )| A. | 1:$\sqrt{2}$ | B. | 1:$\sqrt{3}$ | C. | 1:2 | D. | 2:3 |

 如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,EF=4,则CD=4.
如图,D、E、F分别为Rt△ABC中AB、AC、BC的中点,EF=4,则CD=4. 如图,已知四边形ABCD是平行四边形,点E,F是对角线BD上的两点,且BE=DF,连接AE,CF.求证:AE∥CF且AE=CF.
如图,已知四边形ABCD是平行四边形,点E,F是对角线BD上的两点,且BE=DF,连接AE,CF.求证:AE∥CF且AE=CF.