题目内容
11．在△ABC中，D，E分別是AB，AC的中点，AC=10．F是DE上一点．连接AF，CF，DF=1，若∠AFC=90°，则BC的长度为12．分析 如图，首先证明EF=5，继而得到DE=6；再证明DE为△ABC的中位线，即可解决问题．
解答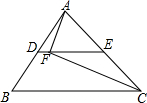 
解：如图，∵∠AFC=90°，AE=CE，
∴EF=$\frac{1}{2}$AC=5，
∴DE=1+5=6；
∵D，E分别是AB，AC的中点，
∴DE为△ABC的中位线，
∴BC=2DE=12，
故答案为：12．
点评 本题主要考查了三角形的中位线定理、直角三角形的性质等几何知识点及其应用问题；牢固掌握三角形的中位线定理、直角三角形的性质等几何知识点是解题的基础和关键．
练习册系列答案
相关题目
1．下列计算中，不正确的是（ ）
| A． | 3$\sqrt{2}$×2$\sqrt{5}$=6$\sqrt{10}$ | B． | 3$\sqrt{6}$÷3$\sqrt{7}$=$\frac{6}{7}$ | C． | $\sqrt{2}$-5$\sqrt{2}$=-4$\sqrt{2}$ | D． | （3$\sqrt{2}$+2$\sqrt{3}$ ）（ 3$\sqrt{2}$-2$\sqrt{3}$）=6 |
2．
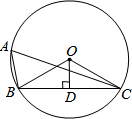如图，⊙O的半径为2，点A为⊙O上一点，半径OD⊥弦BC于D，如果∠BAC=60°，那么OD的长是（ ）
如图，⊙O的半径为2，点A为⊙O上一点，半径OD⊥弦BC于D，如果∠BAC=60°，那么OD的长是（ ）| A． | 2 | B． | $\sqrt{3}$ | C． | 1 | D． | $\frac{\sqrt{3}}{2}$ |
如图，已知四边形ABCD是平行四边形，点E，F是对角线BD上的两点，且BE=DF，连接AE，CF．求证：AE∥CF且AE=CF．
6．在以下四张图片中任意抽取一张，抽到的图片是轴对称图形的有（ ）个．
| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
16．
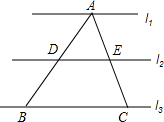如图，l1∥l2∥l3，其中l1与l2、l2与l3间的距离相等，则下列结论：①BC=2DE；②△ADE∽△ABC；③$\frac{AD}{AE}=\frac{AB}{AC}$．其中正确的有（ ）
如图，l1∥l2∥l3，其中l1与l2、l2与l3间的距离相等，则下列结论：①BC=2DE；②△ADE∽△ABC；③$\frac{AD}{AE}=\frac{AB}{AC}$．其中正确的有（ ）| A． | 3个 | B． | 2个 | C． | 1个 | D． | 0个 |
20．
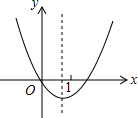已知抛物线y=ax2+bx+c的图象如图所示，则|a-b+c|+|2a+b|=（ ）
已知抛物线y=ax2+bx+c的图象如图所示，则|a-b+c|+|2a+b|=（ ）| A． | a+b | B． | a-2b | C． | a-b | D． | 3a |
1．
如图是一个正方体的平面展开图，把展开图折叠成正方体后，“美”字一面相对面的字是（ ）
如图是一个正方体的平面展开图，把展开图折叠成正方体后，“美”字一面相对面的字是（ ）| A． | 丽 | B． | 连 | C． | 云 | D． | 港 |