题目内容
19.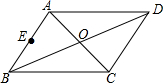 已知,如图平行四边形ABCD中,对角线AC、BD交于点O,点E是AB边上一点,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OE}$=$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$),那么$\overrightarrow{OE}$和$\overrightarrow{BC}$是平行向量吗?为什么?
已知,如图平行四边形ABCD中,对角线AC、BD交于点O,点E是AB边上一点,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OE}$=$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$),那么$\overrightarrow{OE}$和$\overrightarrow{BC}$是平行向量吗?为什么?
分析 首先由平行四边形ABCD中,$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,求得$\overrightarrow{CB}$,又由$\overrightarrow{OE}$=$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$),即可证得$\overrightarrow{OE}$和$\overrightarrow{BC}$是平行向量.
解答 解:$\overrightarrow{OE}$和$\overrightarrow{BC}$是平行向量.
理由:∵四边形ABCD是平行四边形,
∴$\overrightarrow{CO}$=$\overrightarrow{OA}$=$\overrightarrow{a}$,
∵$\overrightarrow{OB}$=$\overrightarrow{b}$,
∴$\overrightarrow{CB}$=$\overrightarrow{CO}$+$\overrightarrow{OB}$=$\overrightarrow{a}$+$\overrightarrow{b}$,
∵$\overrightarrow{OE}$=$\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$),
∴$\overrightarrow{OE}$和$\overrightarrow{BC}$是平行向量.
点评 此题考查了平行向量的知识.注意掌握三角形法则的应用与平行四边形的性质是解此题的关键.

练习册系列答案
相关题目
9.下列方程中,是关于x的一元二次方程的是( )
| A. | 3(x+1)2=2(x+1) | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | C. | ax2+bx+c=0 | D. | x2-2x=x2+1 |
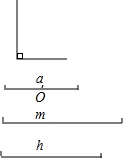 如图所示,已知线段a,m,h(m>h),O为线段a的中点,一个90°角,
如图所示,已知线段a,m,h(m>h),O为线段a的中点,一个90°角,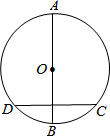 如图⊙O,AB是它的直径,DC是它上面的一条弦,已知DC=6,AB⊥DC,圆心O到DC的距离为4,则圆的半径是( )
如图⊙O,AB是它的直径,DC是它上面的一条弦,已知DC=6,AB⊥DC,圆心O到DC的距离为4,则圆的半径是( )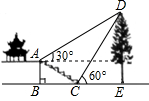 某班数学课外活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度i=1:2,且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测倾器的高度忽略不计,结果保留根号)
某班数学课外活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处测得树顶端D的仰角为60°,已知A点的高度AB为2米,台阶AC的坡度i=1:2,且B,C,E三点在同一条直线上,请根据以上条件求出树DE的高度.(测倾器的高度忽略不计,结果保留根号)