不等式组$\left\{\begin{array}{l}{3x+1＞0}\\{2x-a＜0}\end{array}\right.$的整数解有2013个.则a的取值范围是4026≤a＜4028．题目和参考答案——青夏教育精英家教网——

题目内容

7．不等式组$\left\{\begin{array}{l}{3x+1＞0}\\{2x-a＜0}\end{array}\right.$的整数解有2013个，则a的取值范围是4026≤a＜4028．

分析首先根据不等式恰好有2013个整数解求出不等式组的解集为-$\frac{1}{3}$＜x＜2013，再确定2013≤$\frac{1}{2}$a＜2014，然后解不等式即可．

解答解：∵不等式组$\left\{\begin{array}{l}{3x+1＞0}\\{2x-a＜0}\end{array}\right.$的解为-$\frac{1}{3}$＜x＜$\frac{1}{2}$a，
∴
∴2013≤$\frac{1}{2}$a＜2014，
解得：4026≤a＜4028．

点评此题主要考查了解不等式组，关键是正确理解解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．

练习册系列答案

快乐AB卷系列答案

轻松赢考期末卷系列答案

全优期末大考卷系列答案

一通百通考点预测期末测试卷系列答案

冲刺100分全程密卷系列答案

成龙计划课时一本通系列答案

名师导学系列答案

南通密卷系列答案

培优计划赢在起跑线系列答案

情景导学系列答案

相关题目

17．下面说法中，正确的是（　　）

	A．	互余的两个角一定不相等
	B．	互补的两个角一定不相等
	C．	互余的两个角之比是1：3，则这两个角分别是20°和60°
	D．	一个锐角的余角比这个角的补角小90°

18．把下列各数填入它所属的集合内：
-56%，+11，$\frac{3}{5}$，-125，+2.5，-$\frac{13}{6}$，0，-$\frac{π}{3}$，-（-1），2-（-5）．
整数集合{+11，-125，0，-（-1），2-（-5）}，分数集合{-56%，$\frac{3}{5}$，+2.5，$-\frac{13}{6}$}，
负分数集合{-56%，-$\frac{13}{6}$}，负有理数集合{-56%，-125，-$-\frac{13}{6}$}，
非负整数集和{+11，0，-（-1），2-（-5）}，非负数集合{+11，$\frac{3}{5}$，+2.5，0，-（-1），2-（-5）}．

15．小刚用配方法解2x²-bx+a=0得x-$\frac{3}{2}$=±$\frac{\sqrt{15}}{2}$，则b的值为（　　）

2．求下列二次函数的最大值或最小值．
（1）y=-x²+2x；
（2）y=2x²-2x+1．

12．计算：
（1）2$\sqrt{3}$×$\root{3}{1.5}$×$\root{6}{12}$
（2）（2$\frac{7}{9}$）^0.5+0.1^-2+（2$\frac{10}{27}$）${\;}^{-\frac{2}{3}}$-3π⁰+$\frac{37}{48}$
（3）$\frac{（3{a}^{\frac{2}{3}}{b}^{\frac{1}{4}}）（-8{a}^{\frac{1}{2}}{b}^{\frac{1}{2}}）}{-4\root{6}{{a}^{4}}•\sqrt{{b}^{3}}}$．

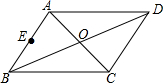已知，如图平行四边形ABCD中，对角线AC、BD交于点O，点E是AB边上一点，$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OE}$=$\frac{1}{2}$（$\overrightarrow{a}$+$\overrightarrow{b}$），那么$\overrightarrow{OE}$和$\overrightarrow{BC}$是平行向量吗？为什么？

16．计算$\sqrt{16}$×$\sqrt{\frac{1}{2}}$+$\sqrt{2}$×$\sqrt{8}$的结果估计在（　　）

17．写出“反证法”证明下列命题的第一步”假设”
（1）互补的两个角不能都大于90°：假设互补的两个角都大于90°；
（2）在△ABC中，至少有两个内角是锐角，假设在△ABC中，只有一个内角是锐角；；
（3）等腰三角形的底角必为锐角，假设等腰三角形的底角不是锐角．