题目内容
20.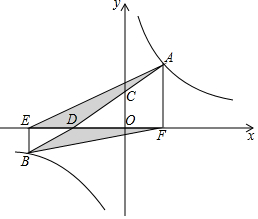 如图,直线AB与双曲线y=$\frac{k}{x}$交于点A,B,与y轴交于点C,与x轴交于点D,过A,B分别作x轴的垂线AF,BE,垂足分别为点F,E,连接AE,BF,若S△ADE+S△BDF=$\frac{3}{2}$k-3,则k的值为( )
如图,直线AB与双曲线y=$\frac{k}{x}$交于点A,B,与y轴交于点C,与x轴交于点D,过A,B分别作x轴的垂线AF,BE,垂足分别为点F,E,连接AE,BF,若S△ADE+S△BDF=$\frac{3}{2}$k-3,则k的值为( )| A. | 3 | B. | 6 | C. | $\sqrt{3}-3$ | D. | 6$\sqrt{2}$ |
分析 设A(m,$\frac{k}{m}$),B(n,$\frac{k}{n}$),得到直线AB的解析式为y=-$\frac{k}{mn}$x+$\frac{(m+n)k}{mn}$,求得D(m+n,0),得到OD=-m-n,DE=m,DF=-n,根据三角形的面积列方程即可得到结论.
解答 解:设A(m,$\frac{k}{m}$),B(n,$\frac{k}{n}$),
∴直线AB的解析式为y=-$\frac{k}{mn}$x+$\frac{(m+n)k}{mn}$,
当y=0时,x=m+n,
∴D(m+n,0),
∴OD=-m-n,
∴DE=m,DF=-n,
∴S△ADE+S△BDF=$\frac{1}{2}$DE•AF+$\frac{1}{2}$DF•BE=$\frac{1}{2}$m•$\frac{k}{m}$$+\frac{1}{2}$(-n)•(-$\frac{k}{n}$)=$\frac{3}{2}$k-3,
∴k=6,
故选B.
点评 本题考查了反比例函数与一次函数的交点问题,三角形面积的计算,求函数的解析式,正确的识别图形是解题的关键.

练习册系列答案
相关题目
3.已知二次函数y=x2-2mx(m为常数),当-1≤x≤2时,函数值y的最小值为-2,则m的值是( )
| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{3}{2}$或$\sqrt{2}$ | D. | $-\frac{3}{2}$或$\sqrt{2}$ |
4.在平行四边形ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则平行四边形ABCD周长是( )
| A. | 22 | B. | 20 | C. | 22或20 | D. | 18 |
8.若关于x的一元二次方程(k-1)x2+2x-2=0有两个不相等的实数根,则k的取值范围是( )
| A. | k>$\frac{1}{2}$ | B. | k≥$\frac{1}{2}$ | C. | k>$\frac{1}{2}$且k≠1 | D. | k≥$\frac{1}{2}$且k≠1 |
15.一次函数y=kx-k(k>0)的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
5.要使二次根式$\sqrt{1-x}$有意义,则x应满足( )
| A. | x≠1 | B. | x≥1 | C. | x≤1 | D. | x<1 |
12.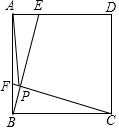 如图,点E、F是边长为4的正方形ABCD边AD、AB上的动点,且AF=DE,BE交CF于点P,在点E、F运动的过程中,PA的最小值为( )
如图,点E、F是边长为4的正方形ABCD边AD、AB上的动点,且AF=DE,BE交CF于点P,在点E、F运动的过程中,PA的最小值为( )
 如图,点E、F是边长为4的正方形ABCD边AD、AB上的动点,且AF=DE,BE交CF于点P,在点E、F运动的过程中,PA的最小值为( )
如图,点E、F是边长为4的正方形ABCD边AD、AB上的动点,且AF=DE,BE交CF于点P,在点E、F运动的过程中,PA的最小值为( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{2}$-2 | D. | 2$\sqrt{5}$-2 |
9.不等式组$\left\{\begin{array}{l}{2-x>1}\\{5x>3(x-2)}\end{array}\right.$的解集是( )
| A. | x>1 | B. | -3<x<1 | C. | x>-3 | D. | 无解 |
10.“岳池米粉”是四川岳池的传统特色小吃之一,距今有三百多年的历史,为了将本地传统小吃推广出去,县领导组织20辆汽车装运A,B,C三种不同品种的米粉42吨到外地销售,按规定每辆车只装同一品种米粉,且必须装满,每种米粉不少于2车.
(1)设x辆车装运A种米粉,用y辆装运B种米粉,根据上表提供的信息,求y与x的函数关系式,并求x的取值范围;
(2)设此次外售活动的利润为w(百元),求w与x的函数关系式以及最大利润,并安排相应的车辆分配方案.
| 米粉品种 | A | B | C |
| 每辆汽车运载量(吨) | 2.2 | 2.1 | 2 |
| 每吨米粉获利(百元) | 6 | 8 | 5 |
(2)设此次外售活动的利润为w(百元),求w与x的函数关系式以及最大利润,并安排相应的车辆分配方案.