题目内容
3.已知二次函数y=x2-2mx(m为常数),当-1≤x≤2时,函数值y的最小值为-2,则m的值是( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{3}{2}$或$\sqrt{2}$ | D. | $-\frac{3}{2}$或$\sqrt{2}$ |
分析 将二次函数配方成顶点式,分m<-1、m>2和-1≤m≤2三种情况,根据y的最小值为-2,结合二次函数的性质求解可得.
解答 解:y=x2-2mx=(x-m)2-m2,
①若m<-1,当x=-1时,y=1+2m=-2,
解得:m=-$\frac{3}{2}$;
②若m>2,当x=2时,y=4-4m=-2,
解得:m=$\frac{3}{2}$<2(舍);
③若-1≤m≤2,当x=m时,y=-m2=-2,
解得:m=$\sqrt{2}$或m=-$\sqrt{2}$<-1(舍),
∴m的值为-$\frac{3}{2}$或$\sqrt{2}$,
故选:D.
点评 本题主要考查二次函数的最值,根据二次函数的增减性分类讨论是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
13.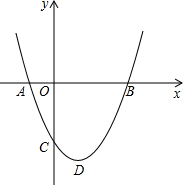 如图,二次函数y=ax2+bx+c图象的顶点D的横坐标为1,其图象与x轴的交点为A、B,3<AB<4,则|a-b+c|+|2a+b+c|=( )
如图,二次函数y=ax2+bx+c图象的顶点D的横坐标为1,其图象与x轴的交点为A、B,3<AB<4,则|a-b+c|+|2a+b+c|=( )
 如图,二次函数y=ax2+bx+c图象的顶点D的横坐标为1,其图象与x轴的交点为A、B,3<AB<4,则|a-b+c|+|2a+b+c|=( )
如图,二次函数y=ax2+bx+c图象的顶点D的横坐标为1,其图象与x轴的交点为A、B,3<AB<4,则|a-b+c|+|2a+b+c|=( )| A. | a-b | B. | 3a+2c | C. | a+2b | D. | -a-b |
14.下列各题计算结果为2a2的是( )
| A. | a6÷a3 | B. | 2a•a | C. | (-2a)2 | D. | (a2)2 |
11.下列二次根式中,是最简二次根式的是( )
| A. | $\sqrt{0.5}$ | B. | $\sqrt{4a}$ | C. | $\sqrt{15}$ | D. | $\sqrt{\frac{1}{3}}$ |
18.随着经济发展,人民的生活水平不断提高,旅游业快速增长,2016年国民出境旅游超过120 000 000人次,将120 000 000用科学记数法表示为( )
| A. | 1.2×109 | B. | 12×107 | C. | 0.12×109 | D. | 1.2×108 |
8.作为世界文化遗产的长城,其总长大约为6700000m.将6700000用科学记数法表示为( )
| A. | 6.7×105 | B. | 6.7×106 | C. | 0.67×107 | D. | 67×108 |
15. 如图,在⊙O中,AB是直径,AC是弦,连接OC,若∠ACO=30°,则∠BOC的度数是( )
如图,在⊙O中,AB是直径,AC是弦,连接OC,若∠ACO=30°,则∠BOC的度数是( )
 如图,在⊙O中,AB是直径,AC是弦,连接OC,若∠ACO=30°,则∠BOC的度数是( )
如图,在⊙O中,AB是直径,AC是弦,连接OC,若∠ACO=30°,则∠BOC的度数是( )| A. | 30° | B. | 45° | C. | 55° | D. | 60° |
12. 如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( )
如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( )
 如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( )
如图,大小不同的两个磁块,其截面都是等边三角形,小三角形边长是大三角形边长的一半,点O是小三角形的内心,现将小三角形沿着大三角形的边缘顺时针滚动,当由①位置滚动到④位置时,线段OA绕点O顺时针转过的角度是( )| A. | 240° | B. | 360° | C. | 480° | D. | 540° |
20.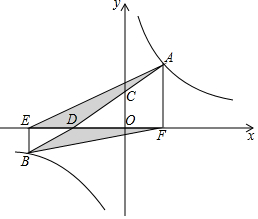 如图,直线AB与双曲线y=$\frac{k}{x}$交于点A,B,与y轴交于点C,与x轴交于点D,过A,B分别作x轴的垂线AF,BE,垂足分别为点F,E,连接AE,BF,若S△ADE+S△BDF=$\frac{3}{2}$k-3,则k的值为( )
如图,直线AB与双曲线y=$\frac{k}{x}$交于点A,B,与y轴交于点C,与x轴交于点D,过A,B分别作x轴的垂线AF,BE,垂足分别为点F,E,连接AE,BF,若S△ADE+S△BDF=$\frac{3}{2}$k-3,则k的值为( )
 如图,直线AB与双曲线y=$\frac{k}{x}$交于点A,B,与y轴交于点C,与x轴交于点D,过A,B分别作x轴的垂线AF,BE,垂足分别为点F,E,连接AE,BF,若S△ADE+S△BDF=$\frac{3}{2}$k-3,则k的值为( )
如图,直线AB与双曲线y=$\frac{k}{x}$交于点A,B,与y轴交于点C,与x轴交于点D,过A,B分别作x轴的垂线AF,BE,垂足分别为点F,E,连接AE,BF,若S△ADE+S△BDF=$\frac{3}{2}$k-3,则k的值为( )| A. | 3 | B. | 6 | C. | $\sqrt{3}-3$ | D. | 6$\sqrt{2}$ |