题目内容
16.(1)用代入法求解$\left\{\begin{array}{l}{2x+3y=16}\\{x+4y=13}\end{array}\right.$(2)用加减消元法求解$\left\{\begin{array}{l}{5x-6y=-3}\\{7x-4y=9}\end{array}\right.$
(3)$\left\{\begin{array}{l}{x+y+z=4}\\{2x-y+z=3}\\{3x-2y-3z=-5}\end{array}\right.$.
分析 (1)代入消元法求解可得;
(2)加减消元法求解可得;
(3)加减消元法求解可得.
解答 解:(1)$\left\{\begin{array}{l}{2x+3y=16}&{①}\\{x+4y=13}&{②}\end{array}\right.$,
由②得x=3-4y ③,
将③代入①得2(13-4y)+3y=16,解得:y=2,
将y=2代入②得:x=5,
∴原方程的解为$\left\{\begin{array}{l}{x=5}\\{y=2}\end{array}\right.$;
(2)用加减消元法求解:
$\left\{\begin{array}{l}{5x-3y=-3}&{①}\\{7x-4y=9}&{②}\end{array}\right.$,
①×2得:10x-12y=-6 ③
②×3得:21x-12y=27④
④-③得:21x-12y-10x+12y=33,解得:x=3,
将x=3代入①得:y=3,
∴原方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$;
(3)$\left\{\begin{array}{l}{x+y+z=4}&{①}\\{2x-y+z=3}&{②}\\{3x-2y-3z=-5}&{③}\end{array}\right.$,
②-①得:x-2y=-1 ④
①×3得,3x+3y+3z=12 ⑤
⑤+③得6x+y=7 ⑥
⑥×2,得:12x+2y=14 ⑦
⑦+④得13x=13,解得:x=1,
将x=1代入④得y=1,
将x=1、y=1代入①得z=2,
∴原方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=1}\\{z=2}\end{array}\right.$.
点评 本题主要考查解二元一次方程组和三元一次方程组,熟练掌握代入消元法和加减消元法是解题的关键.

 计算高手系列答案
计算高手系列答案
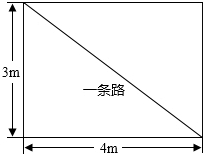 在“寻找滨河最美,拒绝不文明行为”系列活动中,细心的董明同学发现:学校六号楼前有一块长方形花圃(如图所示),有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,请你计算,他们仅仅少走了4步路(假设2步为1米),却踩伤了花草.
在“寻找滨河最美,拒绝不文明行为”系列活动中,细心的董明同学发现:学校六号楼前有一块长方形花圃(如图所示),有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,请你计算,他们仅仅少走了4步路(假设2步为1米),却踩伤了花草.