题目内容
7.已知|x|=5,|y|=1,那么|x-y|-|x+y|=±2.分析 根据题意,利用绝对值的代数意义求出x与y的值,代入原式计算即可得到结果.
解答 解:∵|x|=5,∴x=5或-5,
∵|y|=1,∴y=1或-1,
①x=5时,y=1时,|x-y|-|x+y|表示5到1点的距离与5点到-1点的距离之差,即4-6=-2;
②x=5时,y=-1时,|x-y|-|x+y|表示5到-1点的距离与5到1点的距离之差,即6-4=2;
③x=-5时,y=1时,|x-y|-|x+y|表示-5点到1点的距离与-5点到-1点的距离之差,即6-4=2;
④x=-5时,y=-1时,|x-y|-|x+y|表示-5点到-1点的距离与-5点到1点的距离之差,即4-6=-2,
综上:|x-y|-|x+y|=±2,
故答案为:±2
点评 此题考查了有理数的加减法,以及绝对值,熟练掌握运算法则及绝对值的代数意义是解本题的关键.

练习册系列答案
相关题目
17.若式子$\sqrt{-a-b}$+$\frac{1}{\sqrt{ab}}$有意义,则点P(a、b)在( )
| A. | 坐标原点 | B. | 第一象限 | C. | 第二象限 | D. | 第三象限 |
2.下列说法正确的是( )
| A. | 绝对值等于本身的数是正数 | B. | -a是负数 | ||
| C. | 有理数不是正数就是负数 | D. | 分数都是有理数 |
12.在下列各组数中,是勾股数的一组是( )
| A. | 0.3,0.4,0.5 | B. | 4,5,6 | C. | $\frac{3}{5}$,$\frac{4}{5}$,1 | D. | 24,45,51 |
19.我们知道:1+3=4,1+3+5=9,1+3+5+7=16,…,观察下面的一列数:-1,2,-3,4,-5,6,…将这些数排成如图的形式,根据其规律猜想:第20行第3个数是( )
| -1 | ||||||
| 2 | -3 | 4 | ||||
| -5 | 6 | -7 | 8 | -9 | ||
| 10 | -11 | 12 | -13 | 14 | -15 | 16 |
| … |
| A. | 363 | B. | 364 | C. | -363 | D. | -364 |
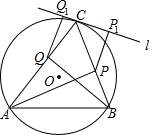 如图,过△ABC的顶点C作这个三角形的外接圆的切线l,AP和BQ即是△ABC的两条高,QQ1⊥l,PP1⊥l,求证:QQ1=PP1.
如图,过△ABC的顶点C作这个三角形的外接圆的切线l,AP和BQ即是△ABC的两条高,QQ1⊥l,PP1⊥l,求证:QQ1=PP1.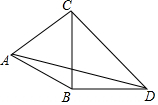 如图,△ABC是等边三角形,∠CBD=90°,BD=DC,则∠BAD的度数是15°.
如图,△ABC是等边三角形,∠CBD=90°,BD=DC,则∠BAD的度数是15°.