题目内容
8.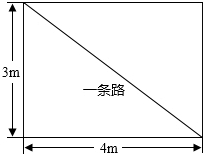 在“寻找滨河最美,拒绝不文明行为”系列活动中,细心的董明同学发现:学校六号楼前有一块长方形花圃(如图所示),有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,请你计算,他们仅仅少走了4步路(假设2步为1米),却踩伤了花草.
在“寻找滨河最美,拒绝不文明行为”系列活动中,细心的董明同学发现:学校六号楼前有一块长方形花圃(如图所示),有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,请你计算,他们仅仅少走了4步路(假设2步为1米),却踩伤了花草.
分析 本题关键是根据勾股定理求出路长,即三角形的斜边长.再求两直角边的和与斜边的差即可求解.
解答 解:根据勾股定理可得斜边长是$\sqrt{{4}^{2}+{3}^{2}}$=5m.
则少走的距离是3+4-5=2m,
∵2步为1米,
∴少走了4步,
故答案为:4.
点评 此题考查了勾股定理的应用,注意单位的换算,通过实际问题向学生渗透思想教育.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
19.我们知道:1+3=4,1+3+5=9,1+3+5+7=16,…,观察下面的一列数:-1,2,-3,4,-5,6,…将这些数排成如图的形式,根据其规律猜想:第20行第3个数是( )
| -1 | ||||||
| 2 | -3 | 4 | ||||
| -5 | 6 | -7 | 8 | -9 | ||
| 10 | -11 | 12 | -13 | 14 | -15 | 16 |
| … |
| A. | 363 | B. | 364 | C. | -363 | D. | -364 |
3.若一个正比例函数的图象经过不同象限的两点A(-2,m),B(n,3),那么一定有( )
| A. | m>0,n>0 | B. | m>0,n<0 | C. | m<0,n>0 | D. | m<0,n<0 |
20.以下结论正确的是( )
| A. | 对角线相等,且一组对角相等的四边形是平行四边形 | |
| B. | 一对邻角的和为180°的四边形是平行四边形 | |
| C. | 一组对边平行且相等的四边形是平行四边形 | |
| D. | 两条对角线相互垂直的四边形是平行四边形 |
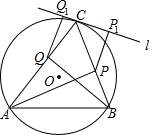 如图,过△ABC的顶点C作这个三角形的外接圆的切线l,AP和BQ即是△ABC的两条高,QQ1⊥l,PP1⊥l,求证:QQ1=PP1.
如图,过△ABC的顶点C作这个三角形的外接圆的切线l,AP和BQ即是△ABC的两条高,QQ1⊥l,PP1⊥l,求证:QQ1=PP1.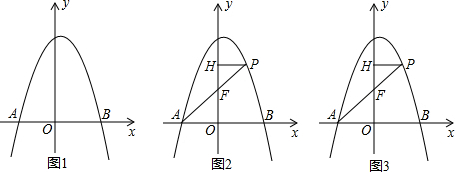
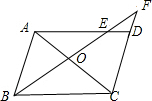 如图,平行四边形ABCD中,过B点作直线交AC、AD于O、E,交CD的延长线于F点,
如图,平行四边形ABCD中,过B点作直线交AC、AD于O、E,交CD的延长线于F点,