题目内容
9.如图1,某超市从一楼到二楼有一自动扶梯,图2是侧面示意图.已知自动扶梯AB的坡度为1:2.4,AB的长度是13米,MN是二楼楼顶,MN∥PQ,C是MN上处在自动扶梯顶端B点正上方的一点,BC⊥MN,在自动扶梯底端A处测得C点的仰角为45°,求二楼的层高BC.
分析 延长CB交PQ于点D,根据坡度的定义即可求得BD的长,然后在直角△CDA中利用三角函数即可求得CD的长,则BC即可得到.
解答  解:如图2,延长CB交PQ于点D.
解:如图2,延长CB交PQ于点D.
∵MN∥PQ,BC⊥MN,
∴BC⊥PQ.
∵自动扶梯AB的坡度为1:2.4,
∴$\frac{BD}{AD}$=$\frac{1}{2.4}=\frac{5}{12}$.
设BD=5k米,AD=12k米,则AB=13k米.
∵AB=13米,
∴k=1,
∴BD=5米,AD=12米.
在Rt△CDA中,∠CDA=90゜,∠CAD=45°,
∴CD=AD=12,
∴BC=12-5=7.
点评 本题考查了解直角三角形的应用,用到的知识点是特殊角的三角函数值、仰角和坡度的定义,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.为了解当地气温变化情况,某研究小组记录了寒假期间连续6天的最高气温,结果如下(单位:℃):-6,-3,x,2,-1,3.若这组数据的中位数是-1,则下列结论错误的是( )
| A. | 方差是8 | B. | 极差是9 | C. | 众数是-1 | D. | 平均数是-1 |
14.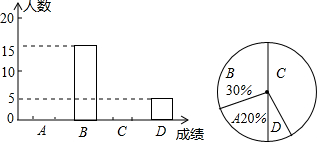 某校九年级一模考试,数学老师为了了解学生的学习情况,随机抽取50名学生的数学成绩进行统计分析,得出相关统计表和统计图如下:
某校九年级一模考试,数学老师为了了解学生的学习情况,随机抽取50名学生的数学成绩进行统计分析,得出相关统计表和统计图如下:
请根据以上所提供的信息回答下列问题:
(1)统计表中的m=10,n=20,并补全条形统计图;
(2)若该校九年级有1000名学生,请据此估计该校九年级一模考试数学成绩在B等级以上(含B等级)的学生有多少名;
(3)针对学生在学习中存在的问题,老师对学生进行了一段时间的针对性复习与训练,若A级学生数可提高40%,B级学生数可提高10%,请估计经过训练后九年级数学成绩在B以上(含B级)的学生可达多少名.
 某校九年级一模考试,数学老师为了了解学生的学习情况,随机抽取50名学生的数学成绩进行统计分析,得出相关统计表和统计图如下:
某校九年级一模考试,数学老师为了了解学生的学习情况,随机抽取50名学生的数学成绩进行统计分析,得出相关统计表和统计图如下:请根据以上所提供的信息回答下列问题:
| 成绩/分 | 111~120 | 101~110 | 91~100 | 90及90以下 |
| 成绩等级 | A | B | C | D |
| 人数 | m | 15 | n | 5 |
(2)若该校九年级有1000名学生,请据此估计该校九年级一模考试数学成绩在B等级以上(含B等级)的学生有多少名;
(3)针对学生在学习中存在的问题,老师对学生进行了一段时间的针对性复习与训练,若A级学生数可提高40%,B级学生数可提高10%,请估计经过训练后九年级数学成绩在B以上(含B级)的学生可达多少名.
19.下列运算正确的是( )
| A. | 3a2-2a2=1 | B. | (a2)3=a5 | C. | a2•a4=a6 | D. | (3a)2=6a2 |
 如图,AB是⊙O的直径,C、G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F.
如图,AB是⊙O的直径,C、G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F. 在一次测量活动中,同学们要测量某公园湖的码头A与它正东方向的亭子B之间的距离,如图.他们选择了与码头A、亭子B在同一水平面上的点P,在点P处测得码头A位于点P北偏西30°方向,亭子B位于点P北偏东43°方向;又测得点P与码头A之间的距离为400米.请你运用以上测得的数据求出码头A与亭子B之间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.7,tan43°≈0.93,sin43°≈0.68.)
在一次测量活动中,同学们要测量某公园湖的码头A与它正东方向的亭子B之间的距离,如图.他们选择了与码头A、亭子B在同一水平面上的点P,在点P处测得码头A位于点P北偏西30°方向,亭子B位于点P北偏东43°方向;又测得点P与码头A之间的距离为400米.请你运用以上测得的数据求出码头A与亭子B之间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.7,tan43°≈0.93,sin43°≈0.68.) 如图所示是一块三角形纸板,其中AD=DF,BE=ED,EF=FC,一只蚂蚁在这张纸上爬行,求蚂蚁踩到阴影部分的概率.
如图所示是一块三角形纸板,其中AD=DF,BE=ED,EF=FC,一只蚂蚁在这张纸上爬行,求蚂蚁踩到阴影部分的概率. 如图,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是$\frac{8\sqrt{3}}{3}$.
如图,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是$\frac{8\sqrt{3}}{3}$.