题目内容
8. 在直角坐标系xoy中,已知抛物线$y=-\frac{{3\sqrt{3}}}{20}({x^2}-\frac{17}{3}x-2)$.
在直角坐标系xoy中,已知抛物线$y=-\frac{{3\sqrt{3}}}{20}({x^2}-\frac{17}{3}x-2)$.(1)求抛物线与x轴的交点坐标;
(2)记抛物线与x轴的右交点为B,点A(1,$\sqrt{3}$)在抛物线上,P、Q两质点分别从A、B两点同时出发,P质点沿AO方向,行驶速度为a个单位/秒、Q质点沿BO方向,行驶速度为2个单位/秒.
①1秒后,P质点到达M点,Q质点到达N点.若要使△OMN与△OAB相似,P质点的行驶速度可以是多少?
②当P质点到达直线OA与抛物线的另一个交点C时,两质点停止行驶.若P质点的行驶速度与Q质点的相同,
记线段MN的平方(MN2)为点M、N的超级距离、t为行驶时间.当t等于多少秒时,质点P、Q之间的超级距离最小.
分析 (1)将解析式写成交点式,即可直接得出交点坐标;
(2)若要使△OMN与△OAB相似,即PQ∥AB时,利用线段比例关系算出AP长度,就可求出速度.
(3)由于点P可以在OA上,也可以在OC上,故分两个时间段分别表示出PQ2,配方求出最小值.注意,在两个范围均求出一个最小值,取最小的一个作为最终答案.
解答 解:(1)∵$y=-\frac{3\sqrt{3}}{20}({x}^{2}-\frac{17}{3}x-2)$=$-\frac{\sqrt{3}}{20}(3{x}^{2}-17x-6)$=$-\frac{\sqrt{3}}{20}(3x+1)(x-6)$,
∴抛物线与x轴的交点为(-$\frac{1}{3}$,0),(6,0),
(2)
①BQ=2,AP=a,
若要使△OMN与△OAB相似,只有一种可能,就是PQ∥AB时,
此时,$\frac{AP}{AO}=\frac{BQ}{OB}=\frac{1}{3}$,
∴AP=$\frac{2}{3}$,
∴a=$\frac{2}{3}$.
②由(1)知B(6,0),
∵A(1,$\sqrt{3}$),
∴OA=2,OA的解析式为:y=$\sqrt{3}$x,∠AOB=60°,
联立方程组:$\left\{\begin{array}{l}{y=\sqrt{3}x}\\{y=-\frac{3\sqrt{3}}{20}({x}^{2}-\frac{17}{3}x-2)}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=1}\\{y=\sqrt{3}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-2}\\{y=-2\sqrt{3}}\end{array}\right.$,
∴C(-2,-2$\sqrt{3}$),
∴OC=4,
∴AC=6,
①当0≤t≤1时,P在OA上,如图1,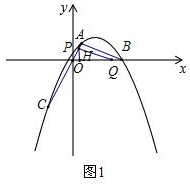
作PH⊥OQ于H,则PA=2t,BQ=2t,OQ=6-2t,OP=2-2t,OH=1-t,PH=$\sqrt{3}$(1-t),HQ=5-t,
∴PQ2=PH2+HQ2=3(1-t)2+(5-t)2=4t2-16+28=4(t-2)2+12,
当t=1时,PQ2最小值为16,
②当1≤t≤3时,P在OC上,如图2,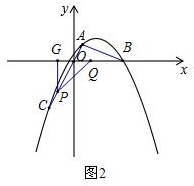
作PG⊥x轴于点G,则OP=2t-2,OQ=6-2t,OG=t-1,PG=$\sqrt{3}$(t-1),GQ=5-t,
∴PQ2=PG2+GQ2=3(t-1)2+(5-t)2=4t2-16+28=4(t-2)2+12,
当t=2,PQ2最小值为12,
综上所述,当t=2时,质点P、Q之间的超级距离最小,最小值为12.
点评 本题考查了二次函数的交点式、相似三角形的判定与性质、特殊角的三角函数、勾股定理,配方法求二次函数最值等重要知识点,难度中等,注意分类讨论思想的应用.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案| A. | 4cm | B. | 7cm | C. | 8cm | D. | 9cm |
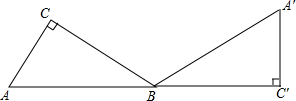 如图,Rt△ABC中,∠C=90°,AB=4,AC=2,将△ABC顺时针旋转至△A′BC′的位置上,使点A,B,C′三点在同一条直线上,则旋转中心是哪一点?旋转角为多少度?
如图,Rt△ABC中,∠C=90°,AB=4,AC=2,将△ABC顺时针旋转至△A′BC′的位置上,使点A,B,C′三点在同一条直线上,则旋转中心是哪一点?旋转角为多少度?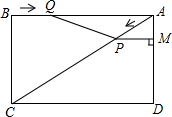 已知:如图,在矩形ABCD中,AC是对角线,AB=4cm,BC=3cm.点P从点A出发,沿AC方向匀速运动,速度为1cm/s,同时,点Q从点B出发,沿BA方向匀
已知:如图,在矩形ABCD中,AC是对角线,AB=4cm,BC=3cm.点P从点A出发,沿AC方向匀速运动,速度为1cm/s,同时,点Q从点B出发,沿BA方向匀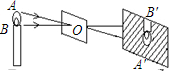 小华做小孔成像实验(如图),已知蜡烛与成像板之间的距离为15cm,则蜡烛与成像板之间的小孔纸板应放在离蜡烛5cm的地方时,蜡烛焰AB是像A′B′的一半.
小华做小孔成像实验(如图),已知蜡烛与成像板之间的距离为15cm,则蜡烛与成像板之间的小孔纸板应放在离蜡烛5cm的地方时,蜡烛焰AB是像A′B′的一半.