题目内容
在Rt△ABC中,∠C=90°,CD是斜边AB上的高,如果CD=3,BD=2.求cos∠A的值.
 【解析】分析:根据题意画出图形,进而利用锐角三角函数关系得出cosA=cos∠BCD进而求出即可.
本题解析:
如图所示:
∵∠ACB=90°,∴∠B+∠A=90°,
∵CD⊥AB,∴∠CDA=90°,∴∠B+∠BCD=90°,∴∠BCD=∠A,
∵CD=3,BD=2,∴BC=
∴cosA=cos∠BCD=
故答案为:
【解析】分析:根据题意画出图形,进而利用锐角三角函数关系得出cosA=cos∠BCD进而求出即可.
本题解析:
如图所示:
∵∠ACB=90°,∴∠B+∠A=90°,
∵CD⊥AB,∴∠CDA=90°,∴∠B+∠BCD=90°,∴∠BCD=∠A,
∵CD=3,BD=2,∴BC=
∴cosA=cos∠BCD=
故答案为:
如图,点B、C、D、E共线,试问图中A、B、C、D、E五点可确定多少个三角形?说明理由.
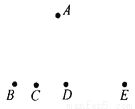
 6个.
【解析】试题分析:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,因而三角形的个数就是B、C、D、E四点中,两个分成一组,点的组数.
试题解析:可以确定6个三角形.
理由:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,
所以图中可以确定6个三角形.
6个.
【解析】试题分析:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,因而三角形的个数就是B、C、D、E四点中,两个分成一组,点的组数.
试题解析:可以确定6个三角形.
理由:经过两点可以确定一条线段,而不在同一条直线上的三条线段首尾顺次相接可组成一个三角形,
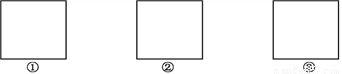
所以图中可以确定6个三角形. 将一个正方形按下列要求割成4块:
(1)分割后的整个图形必须是轴对称图形;
(2)所分得的4块图形是全等图形.
请你按照上述两个要求,分别在图①,②,③中的正方形中画出3种不同的分割方法.(不写画法)
 答案不唯一,
【解析】分割后的整个图形必须是轴对称图形,作两边的中垂线;四块图形的完全相同,作法较多,符合要求即可.
【解析】
如图所示.
答案不唯一,
【解析】分割后的整个图形必须是轴对称图形,作两边的中垂线;四块图形的完全相同,作法较多,符合要求即可.
【解析】
如图所示. 如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门BC打开的宽度为2米,以下哪辆车可以通过?( )(栏杆宽度,汽车反光交镜忽略不计)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,车辆尺寸:长×宽×高)
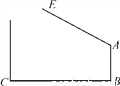
A. 宝马Z4(4200 mm×1800 mm×1360 mm) B. 奇瑞QQ(4000 mm×1600 mm×1520 mm)
C. 大众朗逸(4600 mm×1700 mm×1400 mm) D. 奥迪A4(4700 mm×1800 mm×1400 mm)
 C
【解析】试题解析:如图,过点A作BC的平行线AG,过点N作NQ⊥BC于Q,交AG于点R,
则∠BAG=90°,
∵∠BAE=127°,∠BAG=90°,
∴∠EAH=∠EAB-∠BAG=37°.
在△NAR中,∠ARN=90°,∠EAG=37°,
当车宽为1.8m,则GR=1.8m,故AR=2-1.8=0.2(m),
∴NR=ARtan37°=0.2×...
C
【解析】试题解析:如图,过点A作BC的平行线AG,过点N作NQ⊥BC于Q,交AG于点R,
则∠BAG=90°,
∵∠BAE=127°,∠BAG=90°,
∴∠EAH=∠EAB-∠BAG=37°.
在△NAR中,∠ARN=90°,∠EAG=37°,
当车宽为1.8m,则GR=1.8m,故AR=2-1.8=0.2(m),
∴NR=ARtan37°=0.2×... 如图所示,△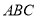 的顶点是正方形网格的格点,则sin
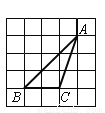
的顶点是正方形网格的格点,则sin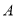 的值为( )
的值为( )
A. 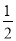 B.
B. 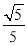 C.
C. 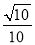 D.
D. 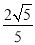
 B
【解析】直接根据题意构造直角三角形,进而利用勾股定理得出DC,AC的长,再利用锐角三角函数关系求出答案.
【解析】
如图所示:连接DC,
由网格可得出∠CDA=90°,
则DC=,AC=,
故sinA===.
故选B.
“点睛”此题主要考查了勾股定理以及锐角三角函数关系,正确构造直角三角形是解题关键.
B
【解析】直接根据题意构造直角三角形,进而利用勾股定理得出DC,AC的长,再利用锐角三角函数关系求出答案.
【解析】
如图所示:连接DC,
由网格可得出∠CDA=90°,
则DC=,AC=,
故sinA===.
故选B.
“点睛”此题主要考查了勾股定理以及锐角三角函数关系,正确构造直角三角形是解题关键. 如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB= .
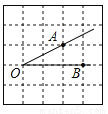
 .
【解析】试题分析:过点A作AD⊥OB垂足为D,如图,在直角△ABD中,AD=1,OD=2,则tan∠AOB==.故答案为: .
.
【解析】试题分析:过点A作AD⊥OB垂足为D,如图,在直角△ABD中,AD=1,OD=2,则tan∠AOB==.故答案为: . 如果∠A为锐角,且sinA=0.6,那么( )
A. 0°<A<30° B. 30°<A<45°
C. 45°<A<60° D. 60°<A<90°
 B
【解析】∵sin30°="1/2," sin45°=,<0.6<
∴30°<∠A<45°,故选B
B
【解析】∵sin30°="1/2," sin45°=,<0.6<
∴30°<∠A<45°,故选B 甲、乙两人沿相同的路线从A到B匀速行驶,A,B两地间的路程为20 km,他们行进的路程s(km)与甲、乙出发的时间t(h)之间关系的图象如图所示,根据图象信息,下列说法正确的是( )
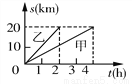
A. 甲的速度是4 km/h B. 乙的速度是10 km/h C. 乙比甲晚出发1 h D. 甲比乙晚到B地3 h
 B
【解析】A. 甲的速度是20÷4=5 km/h,故不正确;
B. 乙的速度是20÷2=10 km/h,故正确;
C. 由图像知,乙和甲同时出发,故不正确;
D. 由图像知,甲比乙晚到B地2 h,故不正确;
故选B.
B
【解析】A. 甲的速度是20÷4=5 km/h,故不正确;
B. 乙的速度是20÷2=10 km/h,故正确;
C. 由图像知,乙和甲同时出发,故不正确;
D. 由图像知,甲比乙晚到B地2 h,故不正确;
故选B. 如图,在△ABC中,点D在BC上,AB=AD=DC,∠B=80°,则∠C的度数为( )

A. 30° B. 40° C. 45° D. 60°
 B
【解析】试题分析:先根据等腰三角形的性质求出∠ADB的度数,再由平角的定义得出∠ADC的度数,根据等腰三角形的性质即可得出结论.
【解析】
∵△ABD中,AB=AD,∠B=80°,
∴∠B=∠ADB=80°,
∴∠ADC=180°﹣∠ADB=100°,
∵AD=CD,
∴∠C===40°.
故选:B.
B
【解析】试题分析:先根据等腰三角形的性质求出∠ADB的度数,再由平角的定义得出∠ADC的度数,根据等腰三角形的性质即可得出结论.
【解析】
∵△ABD中,AB=AD,∠B=80°,
∴∠B=∠ADB=80°,
∴∠ADC=180°﹣∠ADB=100°,
∵AD=CD,
∴∠C===40°.
故选:B. 
