题目内容
甲、乙两人沿相同的路线从A到B匀速行驶,A,B两地间的路程为20 km,他们行进的路程s(km)与甲、乙出发的时间t(h)之间关系的图象如图所示,根据图象信息,下列说法正确的是( )
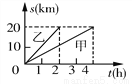
A. 甲的速度是4 km/h B. 乙的速度是10 km/h C. 乙比甲晚出发1 h D. 甲比乙晚到B地3 h
 B
【解析】A. 甲的速度是20÷4=5 km/h,故不正确;
B. 乙的速度是20÷2=10 km/h,故正确;
C. 由图像知,乙和甲同时出发,故不正确;
D. 由图像知,甲比乙晚到B地2 h,故不正确;
故选B.
B
【解析】A. 甲的速度是20÷4=5 km/h,故不正确;
B. 乙的速度是20÷2=10 km/h,故正确;
C. 由图像知,乙和甲同时出发,故不正确;
D. 由图像知,甲比乙晚到B地2 h,故不正确;
故选B.
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案(1)请指出小明的作业(如图)从哪一步开始出现错误,更正过来,并计算出正确结果;
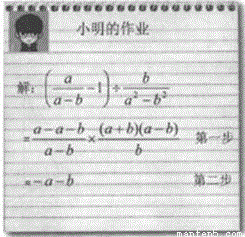
(2)若a,b是不等式组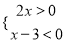 的整数解(a<b),求(1)中分式的值.
的整数解(a<b),求(1)中分式的值.
 (1)小明第一步中括号内计算错了,a+b;(2)3
【解析】试题分析:(1)根据题意,先算括号里面的(通分后进行相减),且把除法转化为乘法,然后约分即可判断错误点,并改错;
(2)通过解不等式组,求出x的取值范围,然后取分母不为0的之代入可求值.
试题解析:(1)小明第一步中括号内计算错了;
原式=×= ×=a+b.
(2)∵解不等式2x>0得x>0,解不等式x-3<...
(1)小明第一步中括号内计算错了,a+b;(2)3
【解析】试题分析:(1)根据题意,先算括号里面的(通分后进行相减),且把除法转化为乘法,然后约分即可判断错误点,并改错;
(2)通过解不等式组,求出x的取值范围,然后取分母不为0的之代入可求值.
试题解析:(1)小明第一步中括号内计算错了;
原式=×= ×=a+b.
(2)∵解不等式2x>0得x>0,解不等式x-3<... 在Rt△ABC中,∠C=90°,CD是斜边AB上的高,如果CD=3,BD=2.求cos∠A的值.
 【解析】分析:根据题意画出图形,进而利用锐角三角函数关系得出cosA=cos∠BCD进而求出即可.
本题解析:
如图所示:
∵∠ACB=90°,∴∠B+∠A=90°,
∵CD⊥AB,∴∠CDA=90°,∴∠B+∠BCD=90°,∴∠BCD=∠A,
∵CD=3,BD=2,∴BC=
∴cosA=cos∠BCD=
故答案为:
【解析】分析:根据题意画出图形,进而利用锐角三角函数关系得出cosA=cos∠BCD进而求出即可.
本题解析:
如图所示:
∵∠ACB=90°,∴∠B+∠A=90°,
∵CD⊥AB,∴∠CDA=90°,∴∠B+∠BCD=90°,∴∠BCD=∠A,
∵CD=3,BD=2,∴BC=
∴cosA=cos∠BCD=
故答案为: 已知sin6°=a,sin36°=b,则sin26°=( )
A. a2 B. 2a C. b2 D. b
 A
【解析】∵sin6°=a,
∴=a2.
故选:A.
A
【解析】∵sin6°=a,
∴=a2.
故选:A. 某种油箱容量为60升的汽车,加满汽油后,汽车行驶时油箱的油量Q(升)随汽车行驶时间t(小时)变化的关系式如下:Q=60-6t.
汽车行驶时间t/小时 | 0 | 1 | 2.5 | 4 | … |
油箱的油量Q/升 | 60 |
(1)请完成下表:
(2)汽车行驶5小时后,油箱中油量是____升;
(3)若汽车行驶过程中,油箱的油量为12升,则汽车行驶了____小时;
(4)贮满60升汽油的汽车,最多行驶____小时;
(5)哪个图象能反映变量Q与t的关系____ .
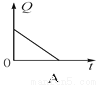
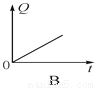
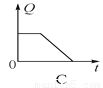
 (1)54,45,36; (2)30; (3)8; (4)10;(5)A
【解析】(1)把t的值依次代入解析式Q=60-6t,可求出Q的值,依次填:54,45,36.
(2)当t=5时,Q=60-6t=60-6×5=30;
(3)当Q=12时,60-6t=12,t=8;
(4)根据题意,当Q=0时,60-6t=0,t=10.所以60升汽油最多行驶10小时.
(5)一次...
(1)54,45,36; (2)30; (3)8; (4)10;(5)A
【解析】(1)把t的值依次代入解析式Q=60-6t,可求出Q的值,依次填:54,45,36.
(2)当t=5时,Q=60-6t=60-6×5=30;
(3)当Q=12时,60-6t=12,t=8;
(4)根据题意,当Q=0时,60-6t=0,t=10.所以60升汽油最多行驶10小时.
(5)一次... 如图,在四边形ABCD中,AC为∠BAD的平分线,AB=AD,点E,F分别在AB,AD上,且AE=DF,请说明为何四边形AECF的面积为四边形ABCD的一半.
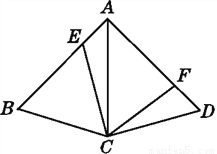
 见解析
【解析】先作CG⊥AB于G,CH⊥AD于H,利用角平分线的性质得出CG=CH,再利用面积间的等量代换即可推出结论.
证明:如图,作CG⊥AB于G,CH⊥AD于H,
因为AC为∠BAD的平分线,
所以CG=CH.
因为AB=AD,
所以S△ABC=S△ACD.
又因为AE=DF,
所以S△AEC=S△CDF.
因为S△BCE=S△ABC-...
见解析
【解析】先作CG⊥AB于G,CH⊥AD于H,利用角平分线的性质得出CG=CH,再利用面积间的等量代换即可推出结论.
证明:如图,作CG⊥AB于G,CH⊥AD于H,
因为AC为∠BAD的平分线,
所以CG=CH.
因为AB=AD,
所以S△ABC=S△ACD.
又因为AE=DF,
所以S△AEC=S△CDF.
因为S△BCE=S△ABC-... 如图,OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,则下列结论错误的是( )
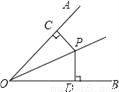
A. PC=PD B. ∠CPD=∠DOP C. ∠CPO=∠DPO D. OC=OD
 B
【解析】试题分析:已知OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,根据角平分线的性质可得PC=PD,A正确;在Rt△OCP与Rt△ODP中,OP=OP,PC=PD,由HL可判定△OCP≌△ODP,根据全等三角形的性质可得∠CPO=∠DPO,OC=OD,故C、D正确.不能得出∠CPD=∠DOP,故B错误.故答案选B.
B
【解析】试题分析:已知OP为∠AOB的角平分线,PC⊥OA,PD⊥OB,垂足分别是C、D,根据角平分线的性质可得PC=PD,A正确;在Rt△OCP与Rt△ODP中,OP=OP,PC=PD,由HL可判定△OCP≌△ODP,根据全等三角形的性质可得∠CPO=∠DPO,OC=OD,故C、D正确.不能得出∠CPD=∠DOP,故B错误.故答案选B. 在Rt△ABC中,∠C=90°,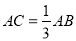 ,则cosA等于( )
,则cosA等于( )
A. 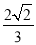 B.
B. 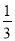 C.
C. 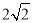 D.
D. 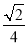
 B
【解析】试题解析:如图所示:
∵,
∴cosA=.
故选B.
B
【解析】试题解析:如图所示:
∵,
∴cosA=.
故选B. 
