题目内容
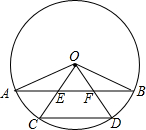 AB、CD是⊙O的弦,OC、OD分别交AB于点E、F,且OE=OF.求证:
AB、CD是⊙O的弦,OC、OD分别交AB于点E、F,且OE=OF.求证: |
| AC |
 |
| BD |
考点:圆心角、弧、弦的关系
专题:证明题
分析:过点O作OG⊥AB于点G,延长OG与⊙O交于H.先由等腰三角形三线合一的性质得出∠EOG=∠FOG,利用圆心角、弧、弦间的关系可以推知
=
;然后根据垂径定理可知
=
;最后根据图形易证得结论.
 |
| CH |
 |
| DH |
 |
| AH |
 |
| BH |
解答: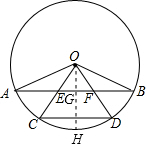 证明:过点O作OG⊥AB于点G,延长OG与⊙O交于H.
证明:过点O作OG⊥AB于点G,延长OG与⊙O交于H.
∵OE=OF,OG⊥EF于点G,
∴∠EOG=∠FOG,
∴
=
.
又∵OG⊥AB于点G,
∴
=
,
∴
-
=
-
,
即
=
.
 证明:过点O作OG⊥AB于点G,延长OG与⊙O交于H.
证明:过点O作OG⊥AB于点G,延长OG与⊙O交于H.∵OE=OF,OG⊥EF于点G,
∴∠EOG=∠FOG,
∴
 |
| CH |
 |
| DH |
又∵OG⊥AB于点G,
∴
 |
| AH |
 |
| BH |
∴
 |
| AH |
 |
| CH |
 |
| BH |
 |
| DH |
即
 |
| AC |
 |
| BD |
点评:本题考查了垂径定理,圆心角、弧、弦的关系,等腰三角形的性质.解答本题时,通过作辅助线OH构建等弧(
=
;
=
)来证明结论.
 |
| CH |
 |
| DH |
 |
| AH |
 |
| BH |

练习册系列答案
相关题目
抛物线y=2+6x-x2的顶点坐标为( )
| A、(3,11) | ||||
| B、(-3,-25) | ||||
C、(
| ||||
| D、(6,2) |
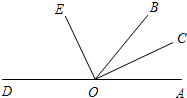 如图,点O是直线AD上一点,射线OC、OE分别是∠AOB、∠BOD的平分线,∠COE=( )°.
如图,点O是直线AD上一点,射线OC、OE分别是∠AOB、∠BOD的平分线,∠COE=( )°.| A、60 | B、70 |
| C、90 | D、不能确定 |
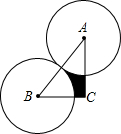 如图在直角△ABC中,∠ACB=90°,AC=8cm,BC=6cm,分别以A、B为圆心,以
如图在直角△ABC中,∠ACB=90°,AC=8cm,BC=6cm,分别以A、B为圆心,以| AB |
| 2 |
A、(24-
| ||
B、
| ||
C、(24-
| ||
D、(24-
|
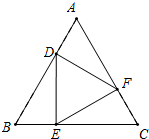 如图,点D、E、F分别在等边△ABC的三边AB、BC、CA上,且△DEF也是等边三角形,求证:AD=BE=CF.
如图,点D、E、F分别在等边△ABC的三边AB、BC、CA上,且△DEF也是等边三角形,求证:AD=BE=CF.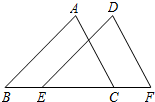 己知:如图,点E、C在线段BF上,BE=CF,AB∥DE,AC∥DF.求证:△ABC≌△DEF.
己知:如图,点E、C在线段BF上,BE=CF,AB∥DE,AC∥DF.求证:△ABC≌△DEF.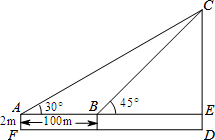 如图,为了测量建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是2m,请你计算出该建筑物的高度.(结果保留根号)
如图,为了测量建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100m,此时自B处测得建筑物顶部的仰角是45°.已知测角仪的高度是2m,请你计算出该建筑物的高度.(结果保留根号)