题目内容
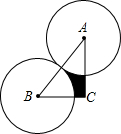 如图在直角△ABC中,∠ACB=90°,AC=8cm,BC=6cm,分别以A、B为圆心,以
如图在直角△ABC中,∠ACB=90°,AC=8cm,BC=6cm,分别以A、B为圆心,以| AB |
| 2 |
A、(24-
| ||
B、
| ||
C、(24-
| ||
D、(24-
|
考点:扇形面积的计算
专题:
分析:根据勾股定理求出AB,则得出圆的半径,分别求出三角形ACB和扇形AEF和扇形BEM的面积和,即可得出答案.
解答: 解:∵在Rt△ACB中,∠C=90°,BC=6,AC=8,由勾股定理得:AB=10,
解:∵在Rt△ACB中,∠C=90°,BC=6,AC=8,由勾股定理得:AB=10,
即两圆的半径是5,
∴阴影部分的面积是S=S△ACB-S扇形AEF-S扇形BEM
=
×6×8-
=24-
π.
故选A.
 解:∵在Rt△ACB中,∠C=90°,BC=6,AC=8,由勾股定理得:AB=10,
解:∵在Rt△ACB中,∠C=90°,BC=6,AC=8,由勾股定理得:AB=10,即两圆的半径是5,
∴阴影部分的面积是S=S△ACB-S扇形AEF-S扇形BEM
=
| 1 |
| 2 |
| 90π×52 |
| 360 |
=24-
| 25 |
| 4 |
故选A.
点评:本题考查了勾股定理,三角形面积,扇形的面积的应用,注意:圆心角是n度,半径是r的扇形的面积S=
.
| nπr2 |
| 360 |

练习册系列答案
相关题目
 如图,DE∥BC,则下列比例式错误的是( )
如图,DE∥BC,则下列比例式错误的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知
=
=
=k,则k的取值为( )
| a |
| b+c |
| b |
| c+a |
| c |
| b+a |
A、
| ||
| B、-1 | ||
C、
| ||
D、-
|
估算实数
的大小时,若使误差小于1,则结果应为( )
| 3 | 90 |
| A、3或4 | B、4或5 |
| C、5或6 | D、9或10 |
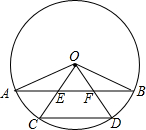 AB、CD是⊙O的弦,OC、OD分别交AB于点E、F,且OE=OF.求证:
AB、CD是⊙O的弦,OC、OD分别交AB于点E、F,且OE=OF.求证:
 如图所示,已知∠1=∠2,DE∥BC,你能判断出图形中还有哪些角是相等的吗?(写出两对相等角即可)
如图所示,已知∠1=∠2,DE∥BC,你能判断出图形中还有哪些角是相等的吗?(写出两对相等角即可) 如图所示,已知AB⊥BC于点B,DC⊥BC于点C,∠1=∠2,请说明BE∥CF的理由.
如图所示,已知AB⊥BC于点B,DC⊥BC于点C,∠1=∠2,请说明BE∥CF的理由.