题目内容
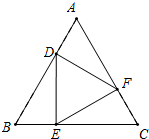 如图,点D、E、F分别在等边△ABC的三边AB、BC、CA上,且△DEF也是等边三角形,求证:AD=BE=CF.
如图,点D、E、F分别在等边△ABC的三边AB、BC、CA上,且△DEF也是等边三角形,求证:AD=BE=CF.考点:全等三角形的判定与性质,等边三角形的性质
专题:证明题
分析:由△ABC是等边三角形,AD=BE=CF,易证得△ADF≌△BED,即可得DF=DE,同理可得DF=EF,即可证得:△DEF是等边三角形.
解答:证明:∵△ABC是等边三角形,
∴AB=BC=AC,
∵AD=BE=CF,
∴AF=BD,
在△ADF和△BED中,
,
∴△ADF≌△BED(SAS),
∴DF=DE,
同理DE=EF,
∴DE=DF=EF.
∴△DEF是等边三角形.
∴AB=BC=AC,
∵AD=BE=CF,
∴AF=BD,
在△ADF和△BED中,
|
∴△ADF≌△BED(SAS),
∴DF=DE,
同理DE=EF,
∴DE=DF=EF.
∴△DEF是等边三角形.
点评:此题考查了等边三角形的判定与性质以及全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 有一个数值转换器,其工作原理如图所示,若输入2,则输出的结果是( )
有一个数值转换器,其工作原理如图所示,若输入2,则输出的结果是( )| A、-8 | B、-6 | C、8 | D、10 |
下列说法正确的是( )
| A、射线PA和射线AP是同一条射线 |
| B、射线OA的长度是12cm |
| C、直线ab、cd相交于点M |
| D、两点确定一条直线 |
若点C在直线AB上,且AC=13,BC=8,则A、B两点间的距离是( )
| A、5 | B、21 |
| C、5或21 | D、无法确定 |
抛物线y=-2(x-3)2+1的顶点坐标是( )
| A、(-3,1) |
| B、(3,1) |
| C、(1,3) |
| D、(1,-3) |
 如图,AD∥BC.
如图,AD∥BC.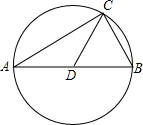 如图所示,CD是△ABC的中线,AB=2CD,∠B=60°.求证:△ABC的外接圆的半径为CB.
如图所示,CD是△ABC的中线,AB=2CD,∠B=60°.求证:△ABC的外接圆的半径为CB. 如图,在△ABC中,AC=BC,以腰AC、BC为边向外作等边△ACD和△BCE,AE与BD相交于点F,连接CF并延长,交AB于点G.求证:
如图,在△ABC中,AC=BC,以腰AC、BC为边向外作等边△ACD和△BCE,AE与BD相交于点F,连接CF并延长,交AB于点G.求证: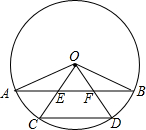 AB、CD是⊙O的弦,OC、OD分别交AB于点E、F,且OE=OF.求证:
AB、CD是⊙O的弦,OC、OD分别交AB于点E、F,且OE=OF.求证: