题目内容
6.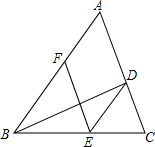 如图,BD是△ABC的角平分线,点E,F分别在边BC,AB上,且DE∥AB,EF∥AC.
如图,BD是△ABC的角平分线,点E,F分别在边BC,AB上,且DE∥AB,EF∥AC.(1)求证:BE=AF;
(2)若∠ABC=56°,∠ADB=120°,求∠AFE的度数.
分析 (1)先证明四边形ADEF是平行四边形,得出对边相等AF=DE,再由平行线的性质和角平分线得出∠DBE=∠BDE,证出BE=DE,即可得出结论;
(2)由角平分线的定义得出∠ABD=∠DBE=28°,再由三角形内角和定理求出∠A的度数,即可得出∠AFE的度数.
解答 (1)证明:∵DE∥AB,EF∥AC,
∴四边形ADEF是平行四边形,∠ABD=∠BDE,
∴AF=DE,
∵BD是△ABC的角平分线,
∴∠ABD=∠DBE,
∴∠DBE=∠BDE,
∴BE=DE,
∴BE=AF;
(2)解:∵BD是△ABC的角平分线,∠ABC=56°,
∴∠ABD=∠DBE=28°,
在△ABD中,∠A=180°-∠ABD-∠ADB=32°,
∵EF∥AC,
∴∠A+∠AFE=180°,
∴∠AFE=180°-∠A=180°-32°=148°.
点评 本题考查了平行四边形的判定与性质、等腰三角形的判定、三角形内角和定理、角平分线、平行线的性质等知识;证明四边形是平行四边形是解决问题的关键,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.下列四个命题中,正确的是( )
| A. | 相似三角形面积的比等于相似比 | |
| B. | 相似三角形对应高的比等于相似比的平方 | |
| C. | 相似三角形对应角平分线的比等于相似比 | |
| D. | 相似三角形中线的比等于相似比 |
 如图,∠AOB=30°,OC平分∠AOB,过点C作CD⊥OA于点D,过点C作CE∥OA交OB于点E.若CE=20cm,求CD的长.
如图,∠AOB=30°,OC平分∠AOB,过点C作CD⊥OA于点D,过点C作CE∥OA交OB于点E.若CE=20cm,求CD的长.
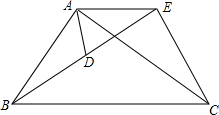 如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,求证:∠ADB=∠AEC.
如图,已知$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,求证:∠ADB=∠AEC.