题目内容
15.二元一次方程组$\left\{\begin{array}{l}{2x-3y=a-4}\\{3x+5y=2-a}\end{array}\right.$的解满足方程x+2y=-6,求a的值及方程组的解.分析 先把三个方程联立求出x、y的值,再代入一个含a的方程求出a的值即可.
解答 解:由题意得$\left\{\begin{array}{l}2x-3y=a-4①\\ 3x+5y=2-a②\\ x+2y=-6③\end{array}\right.$,
①+②得,5x+2y=-2④,
④-③得,4x=4,解得x=1,
代入③得,1+2y=-6,解得y=-$\frac{7}{2}$,
把x=1,y=-$\frac{7}{2}$代入①得,2+$\frac{21}{2}$=a-4,解得a=$\frac{23}{2}$.
故a=$\frac{23}{2}$.
故方程组的解为$\left\{\begin{array}{l}x=1\\ y=-\frac{7}{2}\end{array}\right.$.
点评 本题考查的是二元一次方程组的解,熟知当遇到有关二元一次方程组的解的问题时,要回到定义中去,通常采用代入法,即将解代入原方程组,这种方法主要用在求方程中的字母系数.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
5.计算-3+8的值是( )
| A. | -5 | B. | -1 | C. | 1 | D. | 5 |
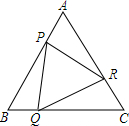 如图所示.△ABC是边长为3的等边三角形,P,Q,R分别是AB,BC,CA上一动点,它们相同的速度,P由A向B运动,Q由B向C运动,R由C向A运动.
如图所示.△ABC是边长为3的等边三角形,P,Q,R分别是AB,BC,CA上一动点,它们相同的速度,P由A向B运动,Q由B向C运动,R由C向A运动.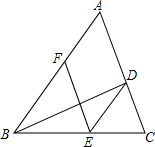 如图,BD是△ABC的角平分线,点E,F分别在边BC,AB上,且DE∥AB,EF∥AC.
如图,BD是△ABC的角平分线,点E,F分别在边BC,AB上,且DE∥AB,EF∥AC.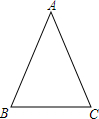 如图,△ABC中,AB=AC=13,BC=10
如图,△ABC中,AB=AC=13,BC=10