题目内容
6．关于x的方程（m+2）x${\;}^{{m}^{2}-2}$+1=0为一元二次方程，则m=2．分析 根据一元二次方程的定义可知，最高次数为2且二次项的系数不为0，即m2-2=2，且m+2≠0，解出m的值即可．
解答 解：由题意可知：m2-2=2，
∴m=±2，
又∵m+2≠0，
∴m≠-2，
即m=2．
故答案为：2
点评 本题考查一元二次方程的定义，要注意系数不为0，这是比较容易漏掉的条件．
练习册系列答案
相关题目
如图，Rt△ABC中，∠BAC=90°，AD⊥BC于D，BE平分∠ABC交AC于E，EF⊥BC于F．求证：EF：DF=BC：AC．
1．
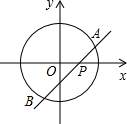如图，在平面直角坐标系中，已知⊙O的半径为2，动直线AB与x轴交于点P（x，0），直线AB与x轴正方向夹角为45°，若直线AB与⊙O有公共点，则x的取值范围是（ ）
如图，在平面直角坐标系中，已知⊙O的半径为2，动直线AB与x轴交于点P（x，0），直线AB与x轴正方向夹角为45°，若直线AB与⊙O有公共点，则x的取值范围是（ ）| A． | -2≤x≤2 | B． | -2$\sqrt{2}$＜x＜2$\sqrt{2}$ | C． | 0≤x≤2$\sqrt{2}$ | D． | -2$\sqrt{2}$≤x≤2$\sqrt{2}$ |
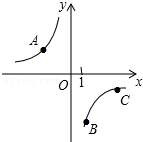如图，A、B、C是反比例函数y=$\frac{k}{x}$（k＜0）图象上三点，作直线l，使点A、B、C到直线l的距离之比为3：1：1，则满足条件的直线l共有（ ）
如图，AB，CD是圆O的直径，且AB⊥CD，P为CD延长线上一点，PE切圆O于E，BE交CD于F，AB=6cm，PE=4cm，则EF的长为$\frac{4\sqrt{10}}{5}$cm．
如图，在两面墙之间有一个底端在A点的梯子，当它靠在一侧墙上时，梯子的顶端在B点．当它靠在另一侧墙上时，梯子的顶端在D点，已知梯子长2.5m，D点到地面的垂直距离DE=1.5m，两墙的距离CE长3.5m．求B点到地面的垂直距离BC．