Question

18．如图，AB，CD是圆O的直径，且AB⊥CD，P为CD延长线上一点，PE切圆O于E，BE交CD于F，AB=6cm，PE=4cm，则EF的长为$\frac{4\sqrt{10}}{5}$cm．

Answer 1

分析 连接OE，可求得∠PEF=∠PFE，可求得PF，在Rt△OBF中由勾股定理可求得BF，再利用相交弦定理可求得EF的长．

解答 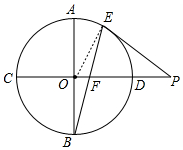解：
如图，连接OE，
∵∠PEF=90°-∠OEB=90°-∠OBE=∠OFB=∠EFP，
∴PF=PE=4，
在Rt△OPE中，由勾股定理可得OP²=PE²+OE²，
∴OP²=3²+4²=25，解得OP=5cm，
∴OF=OP-PF=5-4=1（cm），DF=OD-OF=2cm，CF=OF+OC=4cm，
在Rt△OBF中，由勾定理可得BF²=OB²+OF²，
即BF²=3²+1²=10，
∴FB=$\sqrt{10}$cm，
又由相交弦定理可知BF•EF=CF•DF，
∴EF=$\frac{4×2}{\sqrt{10}}$=$\frac{4\sqrt{10}}{5}$cm，
故答案为：$\frac{4\sqrt{10}}{5}$．

点评 本题主要考查切线的性质及垂径定理，证得PE=PF是解题的关键．