题目内容
9.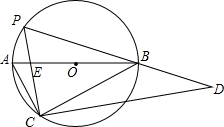 如图,直角△ABC内接于⊙O,∠C=90°,点P在弧AB上移动,P,C分别位于AB的异侧(P不与A,B重合),△PCD也为直角三角形,∠PCD=90°,且直角△PCD的斜边PD经过点B,BA,PC相交于点E.
如图,直角△ABC内接于⊙O,∠C=90°,点P在弧AB上移动,P,C分别位于AB的异侧(P不与A,B重合),△PCD也为直角三角形,∠PCD=90°,且直角△PCD的斜边PD经过点B,BA,PC相交于点E.(1)当BA平分∠PBC时,求$\frac{BE}{CD}$的值;
(2)已知:AC=1,BC=2,求△PCD面积的最大值.
分析 (1)根据圆周角定理得到∠PBA=∠CBA=∠ACP,证得∠BCD=∠CBA,根据平行线的性质得到∠BCD=∠BDC,根据等腰直角三角形的性质得到BC=BD,根据直角三角形的性质得到PB=BC,推出BE是△PCD的中位线,于是得到结论;
(2)根据相似三角形的性质得到$\frac{PC}{CD}=\frac{AC}{CB}=\frac{1}{2}$,由三角形的面积公式得到S△PCD=$\frac{1}{2}$PC•CD=$\frac{1}{2}$PC•2PC=PC2,当CP最大时,△PCD的面积最大,即PC为⊙O的直径时,△PCD的面积最大,即可得到结论.
解答 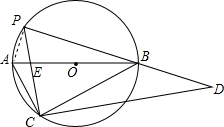 解:(1)连接PA,
解:(1)连接PA,
∴∠PBA=∠CBA=∠ACP,
∵∠ACP=∠BCD,
∴∠BCD=∠CBA,
∴AB∥CD,
∴∠BCD=∠BDC,
∴BC=BD,
∵∠PCD=90°,
∴PB=BC,
∴BE是△PCD的中位线,
∴$\frac{BE}{CD}$=$\frac{1}{2}$;
(2)∵∠PCD=∠ACB=90°,∠ABC=∠D,
∴△ABC∽△PCD,
∴$\frac{PC}{CD}=\frac{AC}{CB}=\frac{1}{2}$,
∴S△PCD=$\frac{1}{2}$PC•CD=$\frac{1}{2}$PC•2PC=PC2,
当CP最大时,△PCD的面积最大,
即PC为⊙O的直径时,△PCD的面积最大,
∴当CP=AB=$\sqrt{5}$时,△PCD的最大面积为($\sqrt{5}$)2=5.
点评 本题考查了三角形的外接圆与外心,等腰三角形的性质,直角三角形的性质,相似三角形的判定和性质,连接AP构造直角三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.生物学家发现一种病毒的长度约为0.000043mm,用科学记数法表示这个数的结果为(单位:mm)( )
| A. | 4.3×10-5 | B. | 4.3×10-4 | C. | 4.3×10-6 | D. | 43×10-5 |
14.若关于x的不等式组$\left\{\begin{array}{l}{x-a≤0}\\{5-2x<1}\end{array}\right.$的整数解只有1个,则a的取值范围是( )
| A. | 2<a<3 | B. | 3≤a<4 | C. | 2<a≤3 | D. | 3<a≤4 |
 用圆规、直尺作图,不写作法,但要保留作图痕迹.
用圆规、直尺作图,不写作法,但要保留作图痕迹. 如图,在同一个平面直角坐标系xOy中,虚半圆O是函数y=$\sqrt{25-{x}^{2}}$(-5≤x≤5)的图象,实曲线(两支)是函数y=$\frac{k}{|x|}$(k≠0)的图象:已知方程$\sqrt{25-{x}^{2}}$=$\frac{k}{|x|}$(k≠0)有一个解为x=-3,则该方程其余的解为3、4、-4.
如图,在同一个平面直角坐标系xOy中,虚半圆O是函数y=$\sqrt{25-{x}^{2}}$(-5≤x≤5)的图象,实曲线(两支)是函数y=$\frac{k}{|x|}$(k≠0)的图象:已知方程$\sqrt{25-{x}^{2}}$=$\frac{k}{|x|}$(k≠0)有一个解为x=-3,则该方程其余的解为3、4、-4.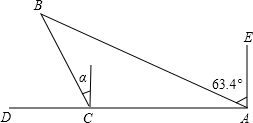 如图,一艘船在海面上由A向D方向航行,在相距4$\sqrt{5}$海里的A、C两地分别测得小岛B在A地的北偏西63.4°方向上,在C地的北偏西26.4°(α=26.4°)方向上,求C点与小岛B之间的距离BC(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin26.6°≈0.45,tan26.6°≈0.5,tan63.6°≈2).
如图,一艘船在海面上由A向D方向航行,在相距4$\sqrt{5}$海里的A、C两地分别测得小岛B在A地的北偏西63.4°方向上,在C地的北偏西26.4°(α=26.4°)方向上,求C点与小岛B之间的距离BC(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin26.6°≈0.45,tan26.6°≈0.5,tan63.6°≈2).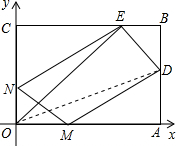 如图所示,已知OABC是一张放在平面直角坐标系中的矩形纸片,O为坐标原点,点A在x轴上,点C在y轴上,且OA=15,OC=9,在边AB上选取一点D,将△AOD沿OD翻折,使点A落在BC边上,记为点E.
如图所示,已知OABC是一张放在平面直角坐标系中的矩形纸片,O为坐标原点,点A在x轴上,点C在y轴上,且OA=15,OC=9,在边AB上选取一点D,将△AOD沿OD翻折,使点A落在BC边上,记为点E.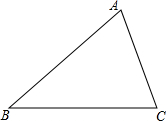 如图,锐角角形ABC中,BC>AB>AC,小骏同学按照下列步骤作图:
如图,锐角角形ABC中,BC>AB>AC,小骏同学按照下列步骤作图: