题目内容
1.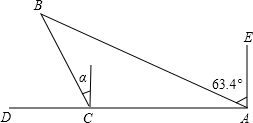 如图,一艘船在海面上由A向D方向航行,在相距4$\sqrt{5}$海里的A、C两地分别测得小岛B在A地的北偏西63.4°方向上,在C地的北偏西26.4°(α=26.4°)方向上,求C点与小岛B之间的距离BC(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin26.6°≈0.45,tan26.6°≈0.5,tan63.6°≈2).
如图,一艘船在海面上由A向D方向航行,在相距4$\sqrt{5}$海里的A、C两地分别测得小岛B在A地的北偏西63.4°方向上,在C地的北偏西26.4°(α=26.4°)方向上,求C点与小岛B之间的距离BC(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin26.6°≈0.45,tan26.6°≈0.5,tan63.6°≈2).
分析 作CF⊥AB于F,根据正弦的概念求出CF,根据正弦的概念计算即可求出BC.
解答 解: 作CF⊥AB于F,
作CF⊥AB于F,
∵AC=4$\sqrt{5}$,∠FAE=63.4°,
∴CF=AC•sin∠CAF=4$\sqrt{5}$×sin26.6°,
∠B=180°-∠A-∠BCA=180°-26.6°-26.4°-90°=37°,
BC=$\frac{CF}{sin∠B}$=$\frac{4\sqrt{5}×0.45}{0.6}$=3$\sqrt{5}$,
答:C点与小岛B之间的距离BC为3$\sqrt{5}$海里.
点评 本题考查的是解直角三角形的应用-方向角问题,正确标注方向角、熟记锐角三角函数的概念是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
12.下列事件中是确定事件的是( )
| A. | 车辆随机经过一个路口,遇到红灯 | |
| B. | 400人中有两人的生日在同一天 | |
| C. | 三条线段可以组成一个三角形 | |
| D. | 任意买一张电影票,座位号是2的倍数 |
10. 由n个相同的小正方体堆成的几何体,其视图如图所示,则n的最小值是( )
由n个相同的小正方体堆成的几何体,其视图如图所示,则n的最小值是( )
 由n个相同的小正方体堆成的几何体,其视图如图所示,则n的最小值是( )
由n个相同的小正方体堆成的几何体,其视图如图所示,则n的最小值是( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
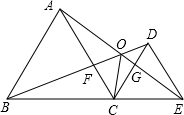 如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连结OC、FG,则下列结论:①AE=BD;②AG=BF;③FG=CG;④∠BOC=∠EOC,⑤FG∥BE.其中结论正确的是①②③④⑤(只填序号)
如图,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连结OC、FG,则下列结论:①AE=BD;②AG=BF;③FG=CG;④∠BOC=∠EOC,⑤FG∥BE.其中结论正确的是①②③④⑤(只填序号)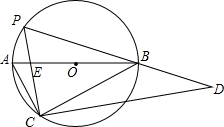 如图,直角△ABC内接于⊙O,∠C=90°,点P在弧AB上移动,P,C分别位于AB的异侧(P不与A,B重合),△PCD也为直角三角形,∠PCD=90°,且直角△PCD的斜边PD经过点B,BA,PC相交于点E.
如图,直角△ABC内接于⊙O,∠C=90°,点P在弧AB上移动,P,C分别位于AB的异侧(P不与A,B重合),△PCD也为直角三角形,∠PCD=90°,且直角△PCD的斜边PD经过点B,BA,PC相交于点E. 解不等式组$\left\{\begin{array}{l}{5+2x≥3}&{①}\\{\frac{x+1}{3}>\frac{x}{2}}&{②}\end{array}\right.$,并把该不等式组的解集表示在数轴上.
解不等式组$\left\{\begin{array}{l}{5+2x≥3}&{①}\\{\frac{x+1}{3}>\frac{x}{2}}&{②}\end{array}\right.$,并把该不等式组的解集表示在数轴上.