题目内容
14.若关于x的不等式组$\left\{\begin{array}{l}{x-a≤0}\\{5-2x<1}\end{array}\right.$的整数解只有1个,则a的取值范围是( )| A. | 2<a<3 | B. | 3≤a<4 | C. | 2<a≤3 | D. | 3<a≤4 |
分析 根据解不等式组的方法可以求出不等式组的解集,又因为关于x的不等式组$\left\{\begin{array}{l}{x-a≤0}\\{5-2x<1}\end{array}\right.$的整数解只有1个,从而可以得到a的取值范围,本题得以解决.
解答 解:$\left\{\begin{array}{l}{x-a≤0}&{①}\\{5-2x<1}&{②}\end{array}\right.$
解不等式①,得x≤a,
解不等式②,得x>2,
故不等式组的解集是2<x≤a,
∵关于x的不等式组$\left\{\begin{array}{l}{x-a≤0}\\{5-2x<1}\end{array}\right.$的整数解只有1个,
∴3≤a<4,
故选B.
点评 本题考查一元一次不等式组的整数解,解题的关键是明确题意,会解一元一次不等式组.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
5. 如图,直线l1∥l2,若∠1=50°,则∠2的度数是( )
如图,直线l1∥l2,若∠1=50°,则∠2的度数是( )
 如图,直线l1∥l2,若∠1=50°,则∠2的度数是( )
如图,直线l1∥l2,若∠1=50°,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 90° | D. | 130° |
19.为了解当地气温变化情况,某研究小组记录了寒假期间连续4天的最高气温,结果如下(单位:℃):
5,-1,-3,-1.则下列结论错误的是( )
5,-1,-3,-1.则下列结论错误的是( )
| A. | 方差是8 | B. | 中位数是-1 | C. | 众数是-1 | D. | 平均数是0 |
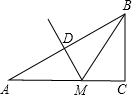 如图,△ABC中,AB的垂直平分线交AC于点M.若AC=8cm,BC=4cm,则△MBC的周长=12cm.
如图,△ABC中,AB的垂直平分线交AC于点M.若AC=8cm,BC=4cm,则△MBC的周长=12cm.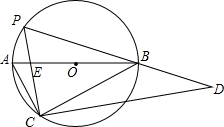 如图,直角△ABC内接于⊙O,∠C=90°,点P在弧AB上移动,P,C分别位于AB的异侧(P不与A,B重合),△PCD也为直角三角形,∠PCD=90°,且直角△PCD的斜边PD经过点B,BA,PC相交于点E.
如图,直角△ABC内接于⊙O,∠C=90°,点P在弧AB上移动,P,C分别位于AB的异侧(P不与A,B重合),△PCD也为直角三角形,∠PCD=90°,且直角△PCD的斜边PD经过点B,BA,PC相交于点E.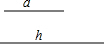 如图,已知两条线段的长度分别为a和h.
如图,已知两条线段的长度分别为a和h.