题目内容
18.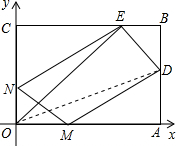 如图所示,已知OABC是一张放在平面直角坐标系中的矩形纸片,O为坐标原点,点A在x轴上,点C在y轴上,且OA=15,OC=9,在边AB上选取一点D,将△AOD沿OD翻折,使点A落在BC边上,记为点E.
如图所示,已知OABC是一张放在平面直角坐标系中的矩形纸片,O为坐标原点,点A在x轴上,点C在y轴上,且OA=15,OC=9,在边AB上选取一点D,将△AOD沿OD翻折,使点A落在BC边上,记为点E.(Ⅰ)求点E和点D的坐标;
(Ⅱ)在x轴、y轴上是否分别存在点M、N,使四边形MNED的周长最小?如果存在,求出点M、N的坐标及四边形MNED周长的最小值;如果不存在,请说明理由.
(Ⅲ)设点P在x轴上,以点O、E、P为顶点的三角形是等腰三角形,请直接写出所有满足条件的点P的坐标.
分析 (Ⅰ)由矩形的性质和勾股定理计算得到点D,E的坐标;
(Ⅱ)做出点D关于x轴的对称点D′,点E关于y轴的对称点E′,连接点D′E′交x,y轴于M,N求找到了周长最小的位置;
(Ⅲ)分四种情况分别根据各自的特点,进行简单的计算即可.
解答 解:(Ⅰ)依题意可OE=OA=15,AD=DE
在Rt△OCE中,CE=12,
∴E(12,9),
又∵BE=BC-CE=3,
在Rt△BED中,DE2=BE2+BD2,
即:DE2=BE2+(9-DE)2
∴DE=AD=5,
∴D(15,5)
(Ⅱ)存在
如图,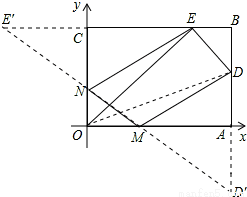
作点D关于x轴的对称点D′(15,-5),E关于y轴的对称点E′(-12,9),
连接点D′E′,分别交x轴、y轴于点M、N,则点M、N即为所求,
设直线D′E′的解析式为y=kx+b,将D′(15,-5)、E′(-12,9)代入得k=-$\frac{14}{27}$,b=$\frac{25}{9}$
∴直线D′E′的解析式为 y=-$\frac{14}{27}$x+$\frac{25}{9}$
令x=0,得y=$\frac{25}{9}$
令y=0,得x=$\frac{75}{14}$
∴M($\frac{75}{14}$,0)、N(0,$\frac{25}{9}$),
在Rt△BE′D′中,D′E′=5$\sqrt{37}$
∴四边形MNED周长最小值=DE+EN+MN+MD=5+5$\sqrt{37}$
(Ⅲ)当在x轴正半轴上,
OP1=OE=15时,点P1与A重合,
∴P1(15,0),
当在x轴负半轴上时,OP2=OE=15时,
P2(-15,0),
如图,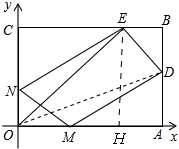
当OE=EP3时,作EH⊥OA,
∴OH=CE=HP3=12,
∴P3(24,0),
当OP4=EP4时,由勾股定理得,P4H2+EH2=P4E2,
∴(12-P4E)2+81=P4E2,
∴OP4=EP4=$\frac{75}{8}$,
∴P4($\frac{75}{8}$,0).
满足条件的P点有四个,分别是P1(15,0),P2(-15,0),P3(24,0),
P4($\frac{75}{8}$,0).
点评 此题是四边形综合题,主要考查了矩形的性质,对折,勾股定理,待定系数法,轴对称,解本题的关键是勾股定理的灵活应用.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案 由n个相同的小正方体堆成的几何体,其视图如图所示,则n的最小值是( )
由n个相同的小正方体堆成的几何体,其视图如图所示,则n的最小值是( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
| A. | a•3 | B. | 2ab2c | C. | $\frac{{a}^{2}b}{4}$ | D. | a×b÷c |
| A. | 2-3=-8 | B. | (2x2)3=8x6 | C. | x6÷x2=x3 | D. | x2+x3=2x5 |
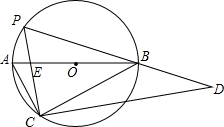 如图,直角△ABC内接于⊙O,∠C=90°,点P在弧AB上移动,P,C分别位于AB的异侧(P不与A,B重合),△PCD也为直角三角形,∠PCD=90°,且直角△PCD的斜边PD经过点B,BA,PC相交于点E.
如图,直角△ABC内接于⊙O,∠C=90°,点P在弧AB上移动,P,C分别位于AB的异侧(P不与A,B重合),△PCD也为直角三角形,∠PCD=90°,且直角△PCD的斜边PD经过点B,BA,PC相交于点E. 解不等式组$\left\{\begin{array}{l}{5+2x≥3}&{①}\\{\frac{x+1}{3}>\frac{x}{2}}&{②}\end{array}\right.$,并把该不等式组的解集表示在数轴上.
解不等式组$\left\{\begin{array}{l}{5+2x≥3}&{①}\\{\frac{x+1}{3}>\frac{x}{2}}&{②}\end{array}\right.$,并把该不等式组的解集表示在数轴上.