题目内容
1.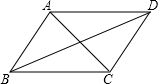 如图,在?ABCD中,已知AB=a,BC=b,∠ABC=α
如图,在?ABCD中,已知AB=a,BC=b,∠ABC=α(1)连接AC,当a=4,b=6,α=60°,求AC的值;
(2)α为锐角,
①连接AC,求证:AC2<a2+b2;
②连接BD,求证:BD2>a2+b2;
(3)连接AC,BD,求证:AC2+BD2=2a2+2b2.
分析 设BE=c,作AE⊥BC于点E,DF⊥BC,交BC延长线于点F,
(1)先确定∠BAE=30°,继而可得AE的长度;
(2)①在Rt△ACE中,运用勾股定理可得AC2=AE2+EC2,继而可得结论;
②在Rt△BDF中,运用勾股定理可得BD2=DF2+BF2,继而可得结论;
(3)由(2)的结论,两式相加即可得出结论.
解答 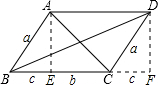 解:如图:设BE=c,作AE⊥BC于点E,DF⊥BC,交BC延长线于点F,
解:如图:设BE=c,作AE⊥BC于点E,DF⊥BC,交BC延长线于点F,
易得:AE=DF,BE=CF,
(1)在Rt△ABE中,
∵∠ABC=60°,
∴∠BAE=30°,
∴BE=$\frac{1}{2}$AB=2,EC=6-2=4,
由勾股定理得:AE=2$\sqrt{3}$,
∴在Rt△ACE中,AC=$\sqrt{{AE}^{2}+C{E}^{2}}$=2$\sqrt{7}$;
(2)①在Rt△ACE中,∵AC2=AE2+EC2=a2-c2+(b-c)2=a2+b2-2bc,
∴AC2<a2+b2;
②在Rt△BDF中,∵BD2=DF2+BF2=a2-c2+(b+c)2=a2+b2+2bc,
∴BD2>a2+b2;
(3)由(2)得:AC2=a2+b2-2bc(A),
BD2=a2+b2+2bc(B),
(A)+(B)=AC2+BD2=2a2+2b2.
点评 本题考查了平行四边形的性质及勾股定理的知识,解答本题得关键是作出辅助线,熟练掌握勾股定理的表达式.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
11.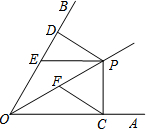 如图,已知OP平分∠AOB,∠AOB=60°,PC⊥OA于点C,PD⊥OB于点D,EP∥OA,交OB于点E,且EP=6.若点F是OP的中点,则CF的长是( )
如图,已知OP平分∠AOB,∠AOB=60°,PC⊥OA于点C,PD⊥OB于点D,EP∥OA,交OB于点E,且EP=6.若点F是OP的中点,则CF的长是( )
 如图,已知OP平分∠AOB,∠AOB=60°,PC⊥OA于点C,PD⊥OB于点D,EP∥OA,交OB于点E,且EP=6.若点F是OP的中点,则CF的长是( )
如图,已知OP平分∠AOB,∠AOB=60°,PC⊥OA于点C,PD⊥OB于点D,EP∥OA,交OB于点E,且EP=6.若点F是OP的中点,则CF的长是( )| A. | 6 | B. | $3\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $3\sqrt{3}$ |

 如图,正方形ABCD、DEFH的边长都是5cm,点P从点D出发,先到点A,然后沿箭头所指方向运动(经过点D时不拐弯),则从出发开始连续运动2014cm时,它离点C 最近,此时它距该点1cm.
如图,正方形ABCD、DEFH的边长都是5cm,点P从点D出发,先到点A,然后沿箭头所指方向运动(经过点D时不拐弯),则从出发开始连续运动2014cm时,它离点C 最近,此时它距该点1cm. 如图,AB是一大型广告牌截面,CD是一堵墙的横截面,AB,CD均与地面BE垂直,广告牌的安全拉线ACE要越过围墙(B、D、E三点在同一直线上),已知:AB=5米,CD=3米,∠CED=45°,∠ACE=165°,求拉线ACE的长l(参考数据$\sqrt{2}$≈1.4)
如图,AB是一大型广告牌截面,CD是一堵墙的横截面,AB,CD均与地面BE垂直,广告牌的安全拉线ACE要越过围墙(B、D、E三点在同一直线上),已知:AB=5米,CD=3米,∠CED=45°,∠ACE=165°,求拉线ACE的长l(参考数据$\sqrt{2}$≈1.4)