题目内容
11.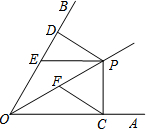 如图,已知OP平分∠AOB,∠AOB=60°,PC⊥OA于点C,PD⊥OB于点D,EP∥OA,交OB于点E,且EP=6.若点F是OP的中点,则CF的长是( )
如图,已知OP平分∠AOB,∠AOB=60°,PC⊥OA于点C,PD⊥OB于点D,EP∥OA,交OB于点E,且EP=6.若点F是OP的中点,则CF的长是( )| A. | 6 | B. | $3\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $3\sqrt{3}$ |
分析 根据两直线平行,同位角相等求出∠DEP,再求出PD,然后根据角平分线上的点到角的两边距离相等可得PC=PD,再求出∠POC=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半求出OP,然后根据直角三角形斜边上的中线等于斜边的一半解答.
解答 解:∵EP∥OA,
∴∠DEP=∠AOB=60°,
∵PD⊥OB,
∴PD=$\frac{\sqrt{3}}{2}$PE=$\frac{\sqrt{3}}{2}$×6=3$\sqrt{3}$,
∵OP平分∠AOB,PC⊥OA,PD⊥OB,
∴PC=PD=3$\sqrt{3}$,
∵OP平分∠AOB,∠AOB=60°,
∴∠POC=$\frac{1}{2}$×60°=30°,
∴OP=2PC=6$\sqrt{3}$,
∵点F是OP的中点,
∴CF=$\frac{1}{2}$OP=$\frac{1}{2}$×6$\sqrt{3}$=3$\sqrt{3}$.
故选D.
点评 本题考查了角平分线上的点到角的两边距离相等,直角三角形30°角所对的直角边等于斜边的一半,直角三角形斜边上的中线等于斜边的一半的性质,熟记各性质并准确识图是解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案
相关题目
6.下列计算中,正确的是( )
| A. | (a2b)3=a6b | B. | a2•a3=a6 | C. | a6÷a3=a3 | D. | ${(\frac{a}{b})^3}=\frac{a^3}{b}$ |
3.为了估计县城空气质量情况,某同学在30天里做了如下记录:
其中w<50时空气质量为优,50≤w≤100时空气质量为良,100<w≤150时空气质量为轻度污染,若1年按365天计算,请你估计该城市在一年中空气质量达到良以上(含良)的天数为292 天.
| 污染指数(w) | 40 | 60 | 80 | 100 | 120 | 140 |
| 天数(天) | 2 | 6 | 9 | 7 | 5 | 1 |
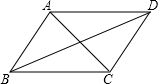 如图,在?ABCD中,已知AB=a,BC=b,∠ABC=α
如图,在?ABCD中,已知AB=a,BC=b,∠ABC=α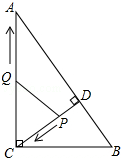 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.