题目内容
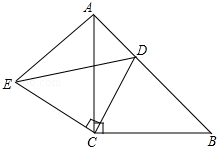
16. 如图,AB是一大型广告牌截面,CD是一堵墙的横截面,AB,CD均与地面BE垂直,广告牌的安全拉线ACE要越过围墙(B、D、E三点在同一直线上),已知:AB=5米,CD=3米,∠CED=45°,∠ACE=165°,求拉线ACE的长l(参考数据$\sqrt{2}$≈1.4)
如图,AB是一大型广告牌截面,CD是一堵墙的横截面,AB,CD均与地面BE垂直,广告牌的安全拉线ACE要越过围墙(B、D、E三点在同一直线上),已知:AB=5米,CD=3米,∠CED=45°,∠ACE=165°,求拉线ACE的长l(参考数据$\sqrt{2}$≈1.4)
分析 过点C作CF⊥AB于点F,在Rt△CDE中求得CE=3$\sqrt{2}$米,在Rt△ACF中求得AC的长相加即可.
解答  解:过点C作CF⊥AB于点F,Rt△CDE中,∠CED=45°,
解:过点C作CF⊥AB于点F,Rt△CDE中,∠CED=45°,
∴CD=DE=3米,∠DCE=45°,
∴CE=3$\sqrt{2}$米,
∵∠ACE=165°,
∴∠ACF=165°-45°-90°=30°,
Rt△ACF中,AF=5-3=2米,
∴AC=2AF=4米,
∴ACE的长l=4+3$\sqrt{2}$≈8.2米.
点评 本题考查了勾股定理的应用,解题的关键是正确的构造三角形,难度不大.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
4. 如图,⊙O是△ABC的外接圆,已知∠A=30°,BC=2,则⊙O的半径为( )
如图,⊙O是△ABC的外接圆,已知∠A=30°,BC=2,则⊙O的半径为( )
 如图,⊙O是△ABC的外接圆,已知∠A=30°,BC=2,则⊙O的半径为( )
如图,⊙O是△ABC的外接圆,已知∠A=30°,BC=2,则⊙O的半径为( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 4 |
5.在同一平面内,下列说法中正确的有( )
①若a∥b,b∥c,则a∥c;
②若a与b相交,b与c相交,则a与c相交;
③若a⊥b,b⊥c,则a⊥c;
④若a∥b,b⊥c,则a⊥c.
①若a∥b,b∥c,则a∥c;
②若a与b相交,b与c相交,则a与c相交;
③若a⊥b,b⊥c,则a⊥c;
④若a∥b,b⊥c,则a⊥c.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.下列计算中,正确的是( )
| A. | (a2b)3=a6b | B. | a2•a3=a6 | C. | a6÷a3=a3 | D. | ${(\frac{a}{b})^3}=\frac{a^3}{b}$ |
 已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.猜想BD2、AD2、CD2之间的关系,并证明.
已知,如图,△ABC和△ECD都是等腰直角三角形,∠ACD=∠DCE=90°,D为AB边上一点.猜想BD2、AD2、CD2之间的关系,并证明.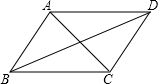 如图,在?ABCD中,已知AB=a,BC=b,∠ABC=α
如图,在?ABCD中,已知AB=a,BC=b,∠ABC=α 如图所示,AB,CD相交于O点,OE是∠COB的平分线,FO⊥OE,且∠AOD=60°.
如图所示,AB,CD相交于O点,OE是∠COB的平分线,FO⊥OE,且∠AOD=60°.