题目内容
在锐角△ABC中,AD、BE分别是BC、AC边上的高,S△ABC=9,S△CDE=1,DE=2,求点C到AB的距离.
考点:面积及等积变换
专题:
分析:利用四点共圆的性质得出∠CED=∠ABC,进而得出△CED∽△ABC,再利用三角形面积公式求出点C到AB的距离.
解答: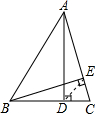 解:∵AD、BE是三角形的高,∴∠AEN=∠ADB=90°,
解:∵AD、BE是三角形的高,∴∠AEN=∠ADB=90°,
∴∠AEB=∠ADB=90°,
∴△ABE和△ABD有以AB为直径的公共外接圆,即四边形ABDE是圆内接四边形,
∴∠CED=∠ABC(圆内接四边形的性质)
又∵∠ACB=∠DCE(公共角)
∴△CED∽△ABC,
∴
=(
)2,即
=
,
∴AB=6(负数舍去),
∴
×6h=9,
解得:h=3,
即点C到AB的距离为3.
 解:∵AD、BE是三角形的高,∴∠AEN=∠ADB=90°,
解:∵AD、BE是三角形的高,∴∠AEN=∠ADB=90°,∴∠AEB=∠ADB=90°,
∴△ABE和△ABD有以AB为直径的公共外接圆,即四边形ABDE是圆内接四边形,
∴∠CED=∠ABC(圆内接四边形的性质)
又∵∠ACB=∠DCE(公共角)
∴△CED∽△ABC,
∴
| S△CED |
| S△ABC |
| DE |
| AB |
| 2 |
| AB2 |
| 1 |
| 9 |
∴AB=6(负数舍去),
∴
| 1 |
| 2 |
解得:h=3,
即点C到AB的距离为3.
点评:此题主要考查了相似三角形的判定与性质以及四点共圆,得出△CED∽△ABC是解题关键.

练习册系列答案
相关题目
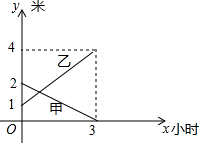 某企业有甲、乙两个长方体的蓄水池,将甲池中的水以每小时6立方米的速度注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示,注水时间为
某企业有甲、乙两个长方体的蓄水池,将甲池中的水以每小时6立方米的速度注入乙池,甲、乙两个蓄水池中水的深度y(米)与注水时间x(时)之间的函数图象如图所示,注水时间为