题目内容
6.实验与探究操作发现:
如图(1)某数学活动小组的同学将正方形A′B′C′O的顶点O与正方形ABCD的中心重合,将正方形A′B′C′O绕点O做旋转实验,发现了如下数学问题:
如图(2),在四边形ABCD中,若AB=AD,∠BAD=∠BCD=90°,则BC、CD、AC具有一定的数量关系:BC+CD=$\sqrt{2}$AC.
数学思考:
(1)请你写出图(2)中数学活动小组的同学发现的结论:BC+CD=AC.(不要求说理或证明)
(2)如图(3),在四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°,则BC、CD、AC具有怎样的数量关系,请给出证明过程.
拓展探究:
如图(4),在四边形ABCD中,AB=AD,∠BAD+∠BCD=180°,且BD=kAB,则BC、CD、AC具有怎样的数量关系?请说明理由.

分析 (1)构造全等三角形,根据邻补角的定义,判断出三角形全等,由△ABD,△BCD为直角三角形,根据勾股定理简单计算即可.
(2)构造全等三角形,根据邻补角的定义,判断出三角形全等,在判断出△AHC为等边三角形即可,
拓展探究:构造全等三角形,从而得出BH=CD,AC=AH,∠BAH=∠DAC,再根据两边对应成比例,夹角相等判断出三角形相似,得出$\frac{HC}{AH}=\frac{BD}{AB}$从而得出结论,
解答 数学思考:(1)故答案为BC+CD=$\sqrt{2}$AC,
(2)BC+CD=AC,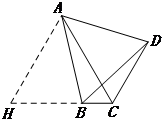
理由:延长CB到H,使BH=CD.
∵∠BAD+∠BCD=60°+120°=180°
∴∠ABC+∠ADC=180°
又∵∠ABH+∠ABC=180°
∴∠ABH=∠ADC
又∵AB=AD
∴△ABH≌△ADC
∴BH=CD,AC=AH,∠BAH=∠DAC
∴∠HAC=∠BAD=60°
∴△AHC为等边三角形
∴BC+CD=BC+BH=AC.
故答案为BC+CD=AC.
拓展探究:
BC+CD=kAC
理由:延长CB到H,使BH=CD.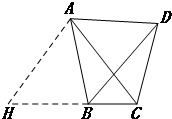
∵∠BAD+∠BCD=180°
∴∠ABC+∠ADC=180°
又∵∠ABH+∠ABC=180°
∴∠ABH=∠ADC
又∵AB=AD
∴△ABH≌△ADC
∴BH=CD,AC=AH,∠BAH=∠DAC
∴∠HAC=∠BAD,$\frac{AH}{AC}=\frac{AB}{AD}$,
∴△AHC∽△ABD
∴$\frac{HC}{AH}=\frac{BD}{AB}$=k,
∴HC=kAH=kAC,
∴BC+CD=kAC.
点评 本题是四边形的综合题,涉及到全等三角形的性质和判定,相似三角形的性质和判定,如:由BH=CD,AC=AH,∠BAH=∠DAC得出∠HAC=∠BAD,$\frac{AH}{AC}=\frac{AB}{AD}$,从而△AHC∽△ABD得到$\frac{HC}{AH}=\frac{BD}{AB}$,勾股定理,等边三角形的判断方法,解本题的关键是构造全等三角形△ABH≌△ADC,本体的难点是作辅助线.

 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案| 购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
| 第一次购物 | 6 | 5 | 1140 |
| 第二次购物 | 3 | 7 | 1110 |
| 第三次购物 | 9 | 8 | 1062 |
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
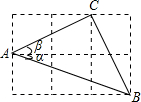 如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(α+β)>tanα+tanβ.(填“>”“=”“<”)
如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(α+β)>tanα+tanβ.(填“>”“=”“<”)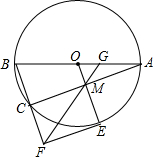 如图,⊙O是△ABC的外接圆,AB为直径,过点O作OM∥BC,交AC于点M.
如图,⊙O是△ABC的外接圆,AB为直径,过点O作OM∥BC,交AC于点M.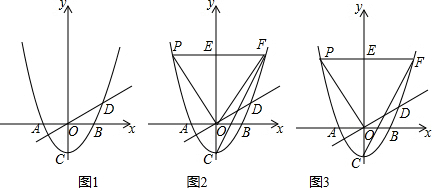
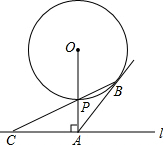 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C. 如图,在?ABCD中,AE=CF,M、N分别是BE、DF 的中点,试说明四边形MFNE是平行四边形.
如图,在?ABCD中,AE=CF,M、N分别是BE、DF 的中点,试说明四边形MFNE是平行四边形.