题目内容
4.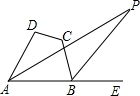 如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=240°,则∠P=30°.
如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=240°,则∠P=30°.
分析 利用四边形内角和是360°可以求得∠DAB+∠ABC=120°.然后由角平分线的性质,邻补角的定义求得∠PAB+∠ABP=$\frac{1}{2}$∠DAB+∠ABC+$\frac{1}{2}$(180°-∠ABC)=90°+$\frac{1}{2}$(∠DAB+∠ABC)的度数,所以根据△ABP的内角和定理求得∠P的度数即可.
解答 解:如图,∵∠D+∠C=240°,∠DAB+∠ABC+∠C+∠D=360°,
∴∠DAB+∠ABC=120°.
又∵∠DAB的角平分线与∠ABC的外角平分线相交于点P,
∴∠PAB+∠ABP=$\frac{1}{2}$∠DAB+∠ABC+$\frac{1}{2}$(180°-∠ABC)=90°+$\frac{1}{2}$(∠DAB+∠ABC)=150°,
∴∠P=180°-(∠PAB+∠ABP)=30°.
故答案是:30.
点评 本题考查了三角形内角和定理、多边形的内角与外角.熟知“四边形的内角和是360°”是解题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
15.生活中我们经常用的梯子,已知长度不变的梯子根地面所成的锐角为α,下面关于α的三角函数与梯子的倾斜程度之间,叙述正确的是( )
| A. | sinα的值越大,梯子越陡 | B. | cosα的值越大,梯子越陡 | ||
| C. | tanα的值越小,梯子越陡 | D. | 陡缓程度与α的函数值无关 |
12.一个等腰三角形的顶角是100°,则它的底角度数是( )
| A. | 30° | B. | 60° | C. | 40° | D. | 不能确定 |
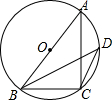 如图,AB是⊙O的直径,C,D是⊙O上的两点(不与A,B重合),若BC=2,tan∠BDC=$\frac{4}{5}$,则AB=$\frac{\sqrt{41}}{2}$.
如图,AB是⊙O的直径,C,D是⊙O上的两点(不与A,B重合),若BC=2,tan∠BDC=$\frac{4}{5}$,则AB=$\frac{\sqrt{41}}{2}$. 如图,点A、B的坐标分别为(1,1)和(5,4),抛物线y=ax2+bx+c(a≠0)的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),当抛物线的顶点为A时,点C的横坐标为O,则点D的横坐标最大值为( )
如图,点A、B的坐标分别为(1,1)和(5,4),抛物线y=ax2+bx+c(a≠0)的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),当抛物线的顶点为A时,点C的横坐标为O,则点D的横坐标最大值为( )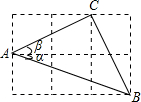 如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(α+β)>tanα+tanβ.(填“>”“=”“<”)
如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(α+β)>tanα+tanβ.(填“>”“=”“<”)