题目内容
5.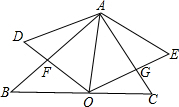 如图,锐角△ABC中,∠BAC=60°,O是BC边上的一点,连接AO,以AO为边向两侧作等边△AOD和等边△AOE,分别与边AB,AC交于点F,G.求证:AF=AG.
如图,锐角△ABC中,∠BAC=60°,O是BC边上的一点,连接AO,以AO为边向两侧作等边△AOD和等边△AOE,分别与边AB,AC交于点F,G.求证:AF=AG.
分析 根据等边三角形的性质得出∠E=∠AOF=60°,AE=AO,∠OAE=60°,求出∠FAO=∠EAG,根据ASA推出△AFO≌△AGE,根据全等三角形的性质得出即可.
解答 证明:∵△AOD和△AOE是等边三角形,
∴∠E=∠AOF=60°,AE=AO,∠OAE=60°,
∵∠BAC=60°,
∴∠FAO=∠EAG=60°-∠CAO,
在△AFO和△AGE中,
$\left\{\begin{array}{l}{∠FAO=∠EAG}\\{AO=AE}\\{∠AOF=∠E}\end{array}\right.$,
∴△AFO≌△AGE(ASA),
∴AF=AG.
点评 本题考查了全等三角形的性质和判定,等边三角形的性质的应用,能求出△AFO≌△AGE是解此题的关键,注意:全等三角形的对应边相等.

练习册系列答案
相关题目
15.生活中我们经常用的梯子,已知长度不变的梯子根地面所成的锐角为α,下面关于α的三角函数与梯子的倾斜程度之间,叙述正确的是( )
| A. | sinα的值越大,梯子越陡 | B. | cosα的值越大,梯子越陡 | ||
| C. | tanα的值越小,梯子越陡 | D. | 陡缓程度与α的函数值无关 |
 如图,点A、B的坐标分别为(1,1)和(5,4),抛物线y=ax2+bx+c(a≠0)的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),当抛物线的顶点为A时,点C的横坐标为O,则点D的横坐标最大值为( )
如图,点A、B的坐标分别为(1,1)和(5,4),抛物线y=ax2+bx+c(a≠0)的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),当抛物线的顶点为A时,点C的横坐标为O,则点D的横坐标最大值为( )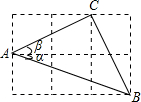 如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(α+β)>tanα+tanβ.(填“>”“=”“<”)
如图,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(α+β)>tanα+tanβ.(填“>”“=”“<”)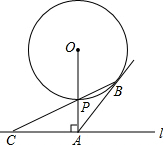 如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.
如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.