题目内容
2.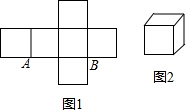 图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方体中的距离是( )
图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方体中的距离是( )| A. | 0 | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 由正方形的性质和勾股定理求出AB的长,即可得出结果.
解答  解:连接AB,如图所示:
解:连接AB,如图所示:
根据题意得:∠ACB=90°,
由勾股定理得:AB=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$;
故选:C.
点评 本题考查了勾股定理、展开图折叠成几何体、正方形的性质;熟练掌握正方形的性质和勾股定理,并能进行推理计算是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.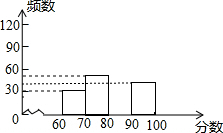 某中学组织全校1500名学生参加安全知识测试,为了解本次测试成绩的分别情况,从中随机抽取了部分学生的成绩,绘制出如图不完整的统计图表:
某中学组织全校1500名学生参加安全知识测试,为了解本次测试成绩的分别情况,从中随机抽取了部分学生的成绩,绘制出如图不完整的统计图表:
请根据以上图表提供的信息,解答下列问题:
(1)表中m的值为200,n的值为0.25;
(2)补全频数分布直方图;
(3)测试成绩的中位数落在哪个分数段?
(4)规定测试成绩80分以上(含80分)为合格,请估计全校学生中合格人数约有多少人?
 某中学组织全校1500名学生参加安全知识测试,为了解本次测试成绩的分别情况,从中随机抽取了部分学生的成绩,绘制出如图不完整的统计图表:
某中学组织全校1500名学生参加安全知识测试,为了解本次测试成绩的分别情况,从中随机抽取了部分学生的成绩,绘制出如图不完整的统计图表:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | 50 | n |
| 80≤x<90 | 80 | 0.4 |
| 90≤x<100 | 40 | 0.2 |
| 合计 | m | 1 |
(1)表中m的值为200,n的值为0.25;
(2)补全频数分布直方图;
(3)测试成绩的中位数落在哪个分数段?
(4)规定测试成绩80分以上(含80分)为合格,请估计全校学生中合格人数约有多少人?
7. 二次函数y=ax2+b的图象如图所示,则下列判断正确的是( )
二次函数y=ax2+b的图象如图所示,则下列判断正确的是( )
 二次函数y=ax2+b的图象如图所示,则下列判断正确的是( )
二次函数y=ax2+b的图象如图所示,则下列判断正确的是( )| A. | a>0,b<0 | B. | a>0,b>0 | C. | a<0,b<0 | D. | a<0,b>0 |
14. 如图,AD是正五边形ABCDE的一条对角线,则∠BAD等于( )
如图,AD是正五边形ABCDE的一条对角线,则∠BAD等于( )
 如图,AD是正五边形ABCDE的一条对角线,则∠BAD等于( )
如图,AD是正五边形ABCDE的一条对角线,则∠BAD等于( )| A. | 72° | B. | 108° | C. | 36° | D. | 62° |
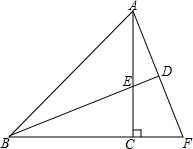 如图,已知等腰直角三角形ABC中,CA=CB,BE平分∠ABC且交AC边于点E,点F在BC的延长线上,∠CAF=∠CBE,延长BE交AF于点D.
如图,已知等腰直角三角形ABC中,CA=CB,BE平分∠ABC且交AC边于点E,点F在BC的延长线上,∠CAF=∠CBE,延长BE交AF于点D. 如图,一只蚂蚁以均匀的速度沿台阶A1→A2→A3→A4→A5爬行,则此蚂蚁爬行的高度h随时间t变化的图象大致是( )
如图,一只蚂蚁以均匀的速度沿台阶A1→A2→A3→A4→A5爬行,则此蚂蚁爬行的高度h随时间t变化的图象大致是( )



