题目内容
12.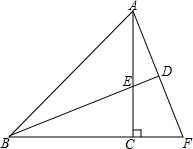 如图,已知等腰直角三角形ABC中,CA=CB,BE平分∠ABC且交AC边于点E,点F在BC的延长线上,∠CAF=∠CBE,延长BE交AF于点D.
如图,已知等腰直角三角形ABC中,CA=CB,BE平分∠ABC且交AC边于点E,点F在BC的延长线上,∠CAF=∠CBE,延长BE交AF于点D.(1)求证:BE=AF;
(2)求证:△BAD∽△AED;
(3)DA与DF相等吗?若相等,请给出证明;若不相等,请说明理由.
分析 (1)根据已知条件证得△BCE≌△ACF,即可得到结论;
(2)由BE平分∠ABC,得到∠ABD=∠DBF,由于∠CAF=∠CBE,得到∠ABD=∠DAE,即可得到结论;
(3)首先证得△ABD≌△FBD,根据全等三角形的性质可得结论AD=DF.
解答 解:(1)在△BCE与△ACF中,
$\left\{\begin{array}{l}{∠EBC=∠FAC}\\{BC=AC}\\{∠BCE=∠ACF=90°}\end{array}\right.$,
∴△BCE≌△ACF,
∴BE=AF;
(2)∵BE平分∠ABC,
∴∠ABD=∠DBF,
∵∠CAF=∠CBE,
∴∠ABD=∠DAE,
∵∠ADE=∠BDA,
∴△BAD∽△ADE;
(3)相等,
∵∠CAF=∠CBE,
∴∠CAF+∠F=∠CBE+∠F=90°,
∴∠BDF=90°,
∴∠ADB=90°,
在△ABD与△FBD中,
$\left\{\begin{array}{l}{∠ABD=∠FBD}\\{BD=BD}\\{∠ADB=∠FDB}\end{array}\right.$,
∴△ABD≌△FBD,
∴AD=DF.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,角平分线的性质等腰三角形的性质,熟练掌握各定理是解题的关键.

练习册系列答案
相关题目
7.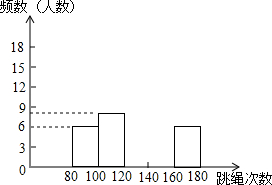 为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:
为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:
请结合图表完成下列问题:
(1)求表中的a;
(2)请把频数分布直方图补充完整;
(3)若七年级学生一分钟跳绳次数(x)达标要求是:80≤x<120不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.为使合格率达到90%,至少还要将几人跳绳水平从不合格提高到合格或合格以上?
 为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:
为进一步了解七年级学生的身体素质请况,老师对七年级(2)班50名学生进行一分钟跳绳次数测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如图所示:| 组 别 | 次 数x | 频数(人数) |
| 第一组 | 80≤x<100 | 6 |
| 第二组 | 100≤x<120 | 8 |
| 第三组 | 120≤x<140 | a |
| 第四组 | 140≤x<160 | 18 |
| 第五组 | 160≤x<180 | 6 |
(1)求表中的a;
(2)请把频数分布直方图补充完整;
(3)若七年级学生一分钟跳绳次数(x)达标要求是:80≤x<120不合格;120≤x<140为合格;140≤x<160为良;x≥160为优.为使合格率达到90%,至少还要将几人跳绳水平从不合格提高到合格或合格以上?
1.下列计算正确的是( )
| A. | a2•a3=a6 | B. | a4÷a4=0 | C. | (-2x)3=-6x3 | D. | (a3)4=a12 |
2.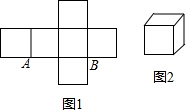 图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方体中的距离是( )
图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方体中的距离是( )
 图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方体中的距离是( )
图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方体中的距离是( )| A. | 0 | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
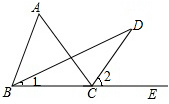 阅读下面的证明过程,在括号内补充推理的依据.
阅读下面的证明过程,在括号内补充推理的依据. 如图,在?ABCD中,对角线AC的垂直平分线交BC于E,交AD于F,求证:四边形AECF的菱形.
如图,在?ABCD中,对角线AC的垂直平分线交BC于E,交AD于F,求证:四边形AECF的菱形.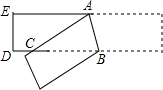 如图,将一张宽为2cm的长方形纸条折叠,折痕为AB,重叠部分为△ABC.如果∠ACB=30°,那么△ABC的面积等于4cm2.
如图,将一张宽为2cm的长方形纸条折叠,折痕为AB,重叠部分为△ABC.如果∠ACB=30°,那么△ABC的面积等于4cm2.