题目内容
13.记M(1)=-2,M(2)=(-2)×(-2),
M(3)=(-2)×(-2)×(-2),…,
M(n)=$\underbrace{(-2)×(-2)×…(-2)}_{n个}$
(1)填空:M(5)=-32,M(1000)是一个正数(填“正数”或“负数”).
(2)计算M(6)+M(7)的值.
(3)当M(n)<0时,求2014M(n)+1007M(n+1)的值.
分析 (1)根据题意确定出所求式子的值即可;
(2)原式根据题意计算即可得到结果;
(3)原式根据题意化简,计算即可得到结果.
解答 解:(1)M(5)=-32,M(1000)是一个正数;
(2)M(6)+M(7)=64-128=-64;
(3)根据题意得:原式=2014×(-2)n+1007×(-2)n+1=2014×(-2)n-2014×(-2)n=0.
故答案为:(1)-32;正数.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
1.下列计算正确的是( )
| A. | a2•a3=a6 | B. | a4÷a4=0 | C. | (-2x)3=-6x3 | D. | (a3)4=a12 |
2.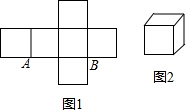 图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方体中的距离是( )
图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方体中的距离是( )
 图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方体中的距离是( )
图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方体中的距离是( )| A. | 0 | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
 阅读下面的证明过程,在括号内补充推理的依据.
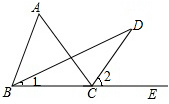
阅读下面的证明过程,在括号内补充推理的依据.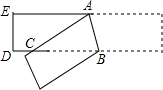 如图,将一张宽为2cm的长方形纸条折叠,折痕为AB,重叠部分为△ABC.如果∠ACB=30°,那么△ABC的面积等于4cm2.
如图,将一张宽为2cm的长方形纸条折叠,折痕为AB,重叠部分为△ABC.如果∠ACB=30°,那么△ABC的面积等于4cm2.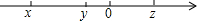 已知实数x、y、z在数轴上的对应点如图所示,化简:$\sqrt{(x-y)^{2}}$-($\sqrt{y-z}$)2+$\root{3}{(x-z)^{3}}$的值.
已知实数x、y、z在数轴上的对应点如图所示,化简:$\sqrt{(x-y)^{2}}$-($\sqrt{y-z}$)2+$\root{3}{(x-z)^{3}}$的值.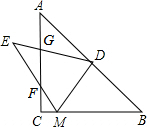 如图,点D是等腰直角△ABC斜边AB的中点,M是边BC上的点,将△DBM沿DM折叠,点B的对称点E落在直线AC的左侧,EM交边AC于点F,ED交边AC于点G.
如图,点D是等腰直角△ABC斜边AB的中点,M是边BC上的点,将△DBM沿DM折叠,点B的对称点E落在直线AC的左侧,EM交边AC于点F,ED交边AC于点G. 如图,已知点A(6,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB、AC相交于点D.当OD=AD=5时,这两个二次函数的最大值之和等于4.
如图,已知点A(6,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB、AC相交于点D.当OD=AD=5时,这两个二次函数的最大值之和等于4.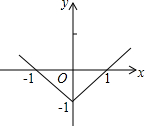 一次函数y=x-1的图象是一条直线,函数y=|x|-1的图象具有怎样的形状呢?
一次函数y=x-1的图象是一条直线,函数y=|x|-1的图象具有怎样的形状呢?