题目内容
10.随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加.据统计,某小区201 1年底拥有家庭轿车640辆,2013年底家庭轿车的拥有量达到1000辆,若该小区2011年底到2014年底家庭轿车拥有量的年平均增长率都相同,求该小区到2014年底家庭轿车将达到多少辆?分析 设家庭轿车拥有量的年平均增长率为x,则增长2次以后的车辆数是6400(1+x)2,列出一元二次方程的解题即可.
解答 解:设家庭轿车拥有量的年平均增长率为x,
则640(1+x)2=1000,
解得x=0.25=25%,或x=-2.25(不合题意,舍去)
∴1000(1+25%)=1250,
答:该小区到2014年底家庭轿车将达到1250辆.
点评 本题考查了一元二次方程的应用.增长率问题:若原数是a,每次增长的百分率为a,则第一次增长后为a(1+x);第二次增长后为a(1+x)2,即 原数×(1+增长百分率)2=后来数.

练习册系列答案
相关题目
1.下列计算正确的是( )
| A. | a2•a3=a6 | B. | a4÷a4=0 | C. | (-2x)3=-6x3 | D. | (a3)4=a12 |
2.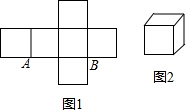 图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方体中的距离是( )
图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方体中的距离是( )
 图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方体中的距离是( )
图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方体中的距离是( )| A. | 0 | B. | 1 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
 如图,在?ABCD中,对角线AC的垂直平分线交BC于E,交AD于F,求证:四边形AECF的菱形.
如图,在?ABCD中,对角线AC的垂直平分线交BC于E,交AD于F,求证:四边形AECF的菱形.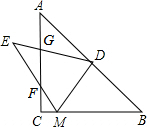 如图,点D是等腰直角△ABC斜边AB的中点,M是边BC上的点,将△DBM沿DM折叠,点B的对称点E落在直线AC的左侧,EM交边AC于点F,ED交边AC于点G.
如图,点D是等腰直角△ABC斜边AB的中点,M是边BC上的点,将△DBM沿DM折叠,点B的对称点E落在直线AC的左侧,EM交边AC于点F,ED交边AC于点G. 如图,已知点A(6,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB、AC相交于点D.当OD=AD=5时,这两个二次函数的最大值之和等于4.
如图,已知点A(6,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB、AC相交于点D.当OD=AD=5时,这两个二次函数的最大值之和等于4. 已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,则点A的对应点A′的坐标是(3,2).
已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,则点A的对应点A′的坐标是(3,2). 如图,在一单位长度为1cm的方格纸上,依如图所示的规律,设定点A1、A2、A3、A4、A5、A6、A7、…、An,连接点O、A1、A2组成三角形,记为△1,连接O、A2、A3组成三角形,记为△2…,连O、An、An+1组成三角形,记为△n(n为正整数),请你推断,当n为50时,△n的面积=( )cm2.
如图,在一单位长度为1cm的方格纸上,依如图所示的规律,设定点A1、A2、A3、A4、A5、A6、A7、…、An,连接点O、A1、A2组成三角形,记为△1,连接O、A2、A3组成三角形,记为△2…,连O、An、An+1组成三角形,记为△n(n为正整数),请你推断,当n为50时,△n的面积=( )cm2. 如图,点E、F在BD上,且AB=CD,BF=DE,AE=CF,AC与BD相交于点O,求证:AE∥CF.
如图,点E、F在BD上,且AB=CD,BF=DE,AE=CF,AC与BD相交于点O,求证:AE∥CF.