Question

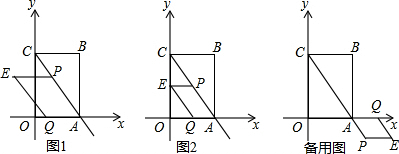
9．在长方形OABC中，OA=6，OC=4，点P是AB边上的点，AP=3，以点O为原点，以OA所在直线为x轴，OC所在直线为y轴，建立如图所示的平面直角坐标系，点Q从原点O出发，以每秒2个单位长度的速度沿着0→A→B→C的路线运动，当点Q运动到点C时停止运动，设运动时间为t．
（1）点B的坐标是（6，4）；
（2）若三角形OPQ的面积是6
①求t的值，
②当点Q在边BC上时，过点Q作QD⊥x轴，交OP于点M，求出点M的坐标．

Answer 1

分析 （1）求出OA、AB的长即可解决问题．
（2）分三种情形讨论即可a、如图1中，当点Q在OA上时．b、如图2中，当点Q在AB上时．C、如图3中，当点Q在BC上时分别列出方程即可解决问题．
（3）求出点Q坐标，以及直线OP的解析式即可解决问题．

解答 解：（1）∵四边形OABC是长方形，
∴AB=OC=4，OC∥AB，
∵OA=6，OC⊥OA，
∴BA⊥OA，
∴点B坐标（6，4）．
故答案为（6，4）．

（2）①如图1中，当点Q在OA上时，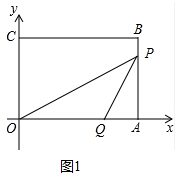

由题意$\frac{1}{2}$×2t×3=6，解得t=2．
如图2中，当点Q在AB上时，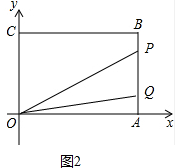

由题意$\frac{1}{2}$×（9-2t）×6=6，
解得t=$\frac{7}{2}$，
如图3中，当点Q在BC上时，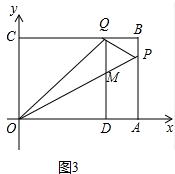

由题意$\frac{4+1}{2}$×6-$\frac{1}{2}$×1×（2t-10）-$\frac{1}{2}$×6×（16-2t）=6，
解得t=6．
综上所述t=2或$\frac{7}{2}$或6秒时，△OPQ的面积为6．

②设直线OP解析式为y=kx，把（6，3）代入得到k=$\frac{1}{2}$，
∴直线OP解析式为y=$\frac{1}{2}$x，
∵点Q在BC上，CQ=4，
∴点Q坐标（4，4），
∴x=4时，y=2，
∴点M坐标（4，2）．

点评 本题考查四边形综合题、矩形的性质、三角形的面积，一次函数等知识，解题的关键是灵活应用这些知识解决问题，学会利用方程去思考问题，属于中考常考题型．